TREE函数:修订间差异
来自Googology Wiki
更多操作
小无编辑摘要 |
无编辑摘要 |
||
| 第4行: | 第4行: | ||
=== 树的嵌入 === | === 树的嵌入 === | ||
[[文件:树的嵌入.png|缩略图]] | |||
给定两棵树<math>A</math>和<math>B</math>,我们称<math>A</math>能嵌入到<math>B</math>中,如果<math>B</math>能通过有限次以下操作得到<math>A</math>: | 给定两棵树<math>A</math>和<math>B</math>,我们称<math>A</math>能嵌入到<math>B</math>中,如果<math>B</math>能通过有限次以下操作得到<math>A</math>: | ||
* 删除一个叶子节点。 | * 删除一个叶子节点。 | ||
* 若某点只有两条边和它连接,删除这个点,用一条边连接与它相邻的两个顶点(即将两条相邻的边合并成一条)。 | * 若某点只有两条边和它连接,删除这个点,用一条边连接与它相邻的两个顶点(即将两条相邻的边合并成一条)。 | ||
例如,图中右边的两棵树均能嵌入到左边的树中,但它们不能互相嵌入。 | |||
=== TREE(n) === | === TREE(n) === | ||
TREE函数研究的是一类特殊的树,其每个顶点被赋予一个值,称为该点的“颜色”。 | |||
给定正整数n,<math>\rm TREE(n)</math>被定义为满足以下条件的“树列”<math>\{T_n\}</math>的最大长度: | 给定正整数n,<math>\rm TREE(n)</math>被定义为满足以下条件的“树列”<math>\{T_n\}</math>的最大长度: | ||
| 第23行: | 第27行: | ||
# <math>T_k</math>至多有<math>n+k</math>个顶点; | # <math>T_k</math>至多有<math>n+k</math>个顶点; | ||
# 对于正整数<math>k<l</math>,<math>T_k</math>不能嵌入到<math>T_l</math>中。 | # 对于正整数<math>k<l</math>,<math>T_k</math>不能嵌入到<math>T_l</math>中。 | ||
== 有限性证明 == | |||
<math>\rm TREE(n)</math>和<math>\rm tree(n)</math>的序列总是有限的,这可由Kruskal树定理保证。 | |||
我们首先要引入'''良拟序(Well-quasi-ordering)'''的概念,它可以看成[[良序]]在一般[[良序#偏序集|偏序集]]上的推广。 | |||
设<math>(X,\le)</math>为一偏序集,若对于<math>X</math>中任意无穷序列<math>x_0,x_1,x_2,\cdots</math>,总存在<math>i<j</math>使得<math>x_i\le x_j</math>,则称<math>\le</math>为集合<math>X</math>上的一个良拟序。 | |||
换句话说,若偏序集中不存在“无穷降链”,也不存在“无穷不可比较链”,则称该偏序为一个良拟序。 | |||
Kruskal树定理说明,树的嵌入关系是一个良拟序。 | |||
也就是说,任意无限棵树构成的序列中,必存在两棵树,前面的树能嵌入到后面的树中。这就证明了<math>\rm tree(n)</math>的有限性。 | |||
== 取值 == | == 取值 == | ||
| 第42行: | 第59行: | ||
=== TREE(3) === | === TREE(3) === | ||
[[文件:TREE(3).jpg|缩略图]] | |||
和<math>\rm TREE(1)</math>、<math>\rm TREE(2)</math>仅有一位数的取值相比,<math>\rm TREE(3)</math>的值出现了“暴涨”,其远远超过了[[葛立恒数]]和[[Kirby-Paris Hydra|Hydra(5)]],这使它成为大数领域中最著名的数字之一。 | 和<math>\rm TREE(1)</math>、<math>\rm TREE(2)</math>仅有一位数的取值相比,<math>\rm TREE(3)</math>的值出现了“暴涨”,其远远超过了[[葛立恒数]]和[[Kirby-Paris Hydra|Hydra(5)]],这使它成为大数领域中最著名的数字之一。 | ||
HypCos在这篇回答<ref>https://www.zhihu.com/question/353941713/answer/885942447</ref>中给出了<math>\rm TREE(3)</math> | 右图是<math>\rm TREE(3)</math>序列可能的前几项。 | ||
HypCos在这篇回答<ref>https://www.zhihu.com/question/353941713/answer/885942447</ref>中给出了<math>\rm TREE(3)</math>的一个下界: | |||
\({\rm TREE(3)}>H_{\varphi(1@\omega,3)\cdot\varphi(1@\omega)}({\rm tree(tree(3)+1)})\)(其中H为[[增长层级#哈代层级|哈代层级]],下同) | \({\rm TREE(3)}>H_{\varphi(1@\omega,3)\cdot\varphi(1@\omega)}({\rm tree(tree(3)+1)})\)(其中H为[[增长层级#哈代层级|哈代层级]],下同) | ||
=== tree(4) === | === tree(4) === | ||
2025年5月24日,HypCos在这篇回答<ref>https://www.zhihu.com/question/1907086430552950742/answer/1909662327449584802</ref>中给出了<math>\rm tree(4)</math>的一个下界: | 2025年5月24日,HypCos在这篇回答<ref>https://www.zhihu.com/question/1907086430552950742/answer/1909662327449584802</ref>中给出了<math>\rm tree(4)</math>的一个下界:<math>{\rm tree(4)}>H_{\varepsilon_{\omega^22+1}+\alpha}(2\uparrow\uparrow\uparrow6)</math> | ||
== 参考资料 == | |||
<references /> | <references /> | ||
[[分类:记号]] | [[分类:记号]] | ||
2025年7月17日 (四) 17:41的版本
TREE函数是由数理逻辑学家Harvey Friedman提出的图论函数。
定义
树的嵌入
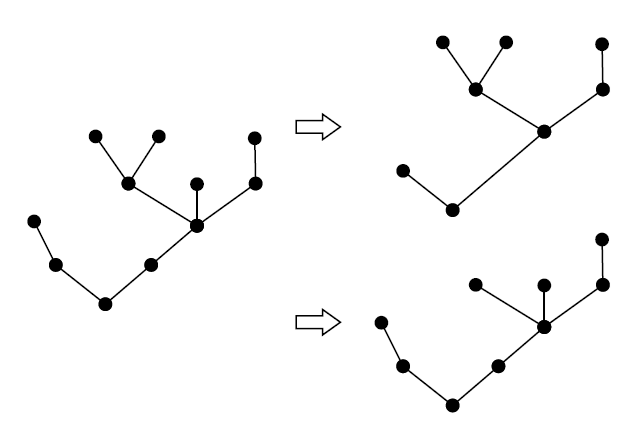
给定两棵树和,我们称能嵌入到中,如果能通过有限次以下操作得到:
- 删除一个叶子节点。
- 若某点只有两条边和它连接,删除这个点,用一条边连接与它相邻的两个顶点(即将两条相邻的边合并成一条)。
例如,图中右边的两棵树均能嵌入到左边的树中,但它们不能互相嵌入。
TREE(n)
TREE函数研究的是一类特殊的树,其每个顶点被赋予一个值,称为该点的“颜色”。
给定正整数n,被定义为满足以下条件的“树列”的最大长度:
- 所有树的顶点至多有种不同的颜色;
- 至多有个顶点;
- 对于正整数,不能嵌入到中。
tree(n)
(注意大小写)被称为弱tree函数,它研究的不是染色树,而是普通树。
给定正整数n,被定义为满足以下条件的“树列”的最大长度:
- 至多有个顶点;
- 对于正整数,不能嵌入到中。
有限性证明
和的序列总是有限的,这可由Kruskal树定理保证。
我们首先要引入良拟序(Well-quasi-ordering)的概念,它可以看成良序在一般偏序集上的推广。
设为一偏序集,若对于中任意无穷序列,总存在使得,则称为集合上的一个良拟序。
换句话说,若偏序集中不存在“无穷降链”,也不存在“无穷不可比较链”,则称该偏序为一个良拟序。
Kruskal树定理说明,树的嵌入关系是一个良拟序。
也就是说,任意无限棵树构成的序列中,必存在两棵树,前面的树能嵌入到后面的树中。这就证明了的有限性。
取值
n较小时
对于,有:
对于,有:
TREE(3)
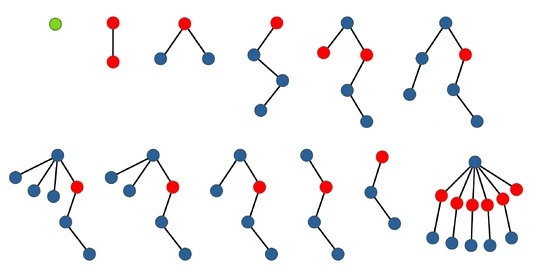
和、仅有一位数的取值相比,的值出现了“暴涨”,其远远超过了葛立恒数和Hydra(5),这使它成为大数领域中最著名的数字之一。
右图是序列可能的前几项。
HypCos在这篇回答[1]中给出了的一个下界:
\({\rm TREE(3)}>H_{\varphi(1@\omega,3)\cdot\varphi(1@\omega)}({\rm tree(tree(3)+1)})\)(其中H为哈代层级,下同)
tree(4)
2025年5月24日,HypCos在这篇回答[2]中给出了的一个下界: