葛立恒数

葛立恒数（Graham's Number）是拉姆齐理论中一个问题（即葛立恒问题）的上界。它也是大数领域中最著名的数之一，与 TREE(3)、SCG(3) 齐名。

定义

葛立恒函数

葛立恒函数（Graham's Function）是用高德纳箭头递归定义的：

$G(n)=\{\begin{array}{ll}3{\uparrow }^{G(n-1)}3& ,n\ne 0\\ 4& ,n=0\end{array}$

葛立恒函数的 FGH 增长率约为$\omega +1$。

葛立恒数

葛立恒数被定义为 $G(64)$（有时也被写作 $G,g_{64},g(64)$ 等）。

$G(64)=\begin{array}{c}3\underbrace{\uparrow \uparrow \cdots \cdots \cdots \cdots \cdots \uparrow }3\\ 3\underbrace{\uparrow \uparrow \cdots \cdots \cdots \cdots \uparrow }3\\ \underbrace{⋮}\\ 3\underbrace{\uparrow \uparrow \cdots \cdots \uparrow }3\\ 3\uparrow \uparrow \uparrow \uparrow 3\end{array}\}\text{64 layers}$

葛立恒问题

葛立恒数源于拉姆齐理论中以下未解决的问题：

考虑一个$n$维的超立方体（1 维为线段，2 维为正方形，3 维为立方体，4 维为超立方体等），

在连结所有顶点后，将形成一个$2^n$个顶点的完全图。将这个图的每条边填上红色或蓝色，求使得所有填法中都必定存在一个在同一平面上有四个顶点的单色完全子图（由四个两两相连的顶点构成，且所有边颜色相同）的$n$的最小值$N^{*}$。

图中展示了一个立方体的示例，包含 12 个共面的 K₄ 完全图，其中下方显示了一个单色 K₄。若将该 K₄ 底部的边改为蓝色，则立方体中将不存在单色的共面 K₄，从而证明 $N^{*}$ 至少为 4。

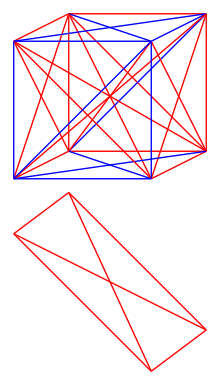
1971 年，R.L.Graham 和 B.L.Rothschild 在他们的论文中证明了$N^{\prime }\le N^{*}\le N$，

其中$N^{\prime }=6$，$N=F(F(F(F(F(F(F(12,3),3),3),3),3),3),3)$。

$F$ 函数的定义为： $F(m,n)=\{\begin{array}{ll}{2}^n& ,m=1\\ 4& ,n=2\\ F(m-1,F(m,n-1))& ,m\ge 2\text{ and }n\ge 3\end{array}$

它等价于 $F^7(12)$ ，其中 $F(n)=2{\uparrow }^{n}3$。

Sbiis Saibian 称这个数字为 “Little Graham”。

目前，该问题有可靠来源的最新下界为$13$，最新上界为

$(2\uparrow \uparrow 5138)\times ((2\uparrow \uparrow 5140)\uparrow \uparrow (2\times 2\uparrow \uparrow 5137))\ll 2\uparrow \uparrow \uparrow 5$。

历史

葛立恒数的由来

从目前的证据来看，葛立恒数的作者并非葛立恒。

1976 年，Donald E.Knuth 在他的论文中定义了现在所使用的高德纳箭头。

1977 年，M.Gardner 在他的文章中定义了现在的葛立恒数。Gardner 在发现这个数字的大小时，发现很难解释，于是他设计了一个更大、更容易解释的数字。他在 Scientific Amercian 上写了关于这个数字的文章，后来在 1980 年作为数学证明中使用的最大数字进入吉尼斯世界纪录，尽管几年后该记录已被删除。一说是 Gardner 在与 Graham 交流后，Graham 给他提供的这个较为宽松的上界，但无从考证，Gardner 的原文章里也没有提及此事。

1995 年，John.H.Conway, Richard.K.Guy 在 The Book of Numbers 一书中给出了葛立恒数，这被许多人认为是它的来源。

葛立恒问题的进展

2003 年，Exoo 证明了 $N^{*}⩾11$。

2008 年，Jerome Barkley 证明了 $N^{*}⩾13$。

2013 年，Mikhail Lavrov, Mitchell Lee, John Mackey 通过使用 Hales-Jewett 定理将上限进一步降低到 $N^{*}=2\uparrow \uparrow 2\uparrow \uparrow (3+2\uparrow \uparrow 8)$。

2019 年，Eryk Lipka 将上限进一步降低到 $(2\uparrow \uparrow 5138)\times ((2\uparrow \uparrow 5140)\uparrow \uparrow (2\times 2\uparrow \uparrow 5137))\ll 2\uparrow \uparrow \uparrow 5$。

比较

由于 $G(0)$ 是 4 而不是 3，因此葛立恒数不能用链式箭头表示法或 BEAF 精确表示。

Tim Chow 证明了葛立恒数比 Moser 数大得多。他于 1998 年 7 月 7 日将证明发送给 Susan Stepney。巧合的是，几天后 Todd Cesere 向 Stepney 发送了类似的证明。

2021年，Daniel Nagaj 声称他的 16 态图灵机实现了多展开并超过了葛立恒数，这意味着 $BB(16)>G(64)$。这一结论后来被 S. Ligocki 证明。

在其他记号中的近似

• $3\to 3\to 64\to 2$（链式箭头表示法）
• $\{3,65,1,2\}$（BEAF）
• $[3,3,4,64]$（Graham Array Notation，精确值）
• $E[3]3\mathrm{\#}\mathrm{\#}4\mathrm{\#}64$（Hyper-E Notation）
• $s(3,64,2,2)$（SAN）
• $64[\mathrm{\&}1]$（Ampersand Notation）
• $f_{\omega +1}(64)$（FGH）
• $H_{{\omega }^{\omega +1}}(64)$ 或 $H_{{\omega }^{\omega }64}(4)$（HH）
• $g_{{\mathrm{\Gamma }}_0}(65)$（SGH）

葛立恒数的最后 n 位

可通过简单的模幂算法轻松计算葛立恒数的最后位数。以下是一个获取较小 x 值对应葛立恒数末 x 位数 N(x) 的简易算法：

$N(x)=\{\begin{array}{ll}3& ,x=0\\ 3^{N(x-1)}(\mathrm{mod}10^x)& ,x\ne 0\end{array}$

然而，若将该公式应用于极大的x值则不成立——尽管该错误公式曾被认为正确，并在 2019 年 12 月前于英语 googology 社区流传。可通过以下思路修正错误：葛立恒数 G(64) 实质是以 3 为底、以极大值 b 为超指数的整数迭代幂次（即 $G(64)={}^{b}3$ )。

2020年，Marco Ripà 证明了在十进制下，当且仅当超指数为 1 时 3 的 congruence speed（同余速度）为 0，否则恒为 1。因此，对所有 $c=1,2,\cdots ,b-2,b-1$， G(64) 的末 b-1 位数与 ${}^{c}3$ 相同。但此性质不适用于 G(64) 的第 b 位数——该数字与 ${}^{b+1}3,{}^{b+2}3,{}^{b+3}3,\cdots$ 的第 b 位数均不相等。由 $b-1={\text{slog}}_3(G_{64})-1$（其中 slog 表示超对数）可得 $G_{63}\ll b-1\ll G_{64}$。故最终可证：对所有正整数 c ，满足：

$G_{64}\equiv {}^{slo{g}_3(G_{64})+c}3(\mathrm{mod}{10}^{slo{g}_3(G_{64})-1})\wedge G_{64}\equiv ̸{}^{slo{g}_3(G_{64})+c}3(\mathrm{mod}{10}^{slo{g}_3(G_{64})})$

实际上，该方法会返回映射 $x\mapsto 3^x$ 在 10 进制整数中的不动点的最后位数。因此上述“错误算法”仅能计算葛立恒数的末 b-1 位。由于 b 值极大（在此尺度下几乎与葛立恒数本身相当），该算法对所有实际应用的 x 值均有效——这可能是其曾被推广至任意正整数 x 的原因。

葛立恒数的最后 1000 位数字如下：

... 69789 01699 96590 70368 75647 69571 41995 17294 68405 82682
71081 20793 88857 60678 08905 76605 97351 28204 06609 18730
71084 83992 11311 79579 18089 16067 30297 76868 73493 26380
38255 18970 12211 05348 18861 41584 87485 19200 98526 10652
52039 48232 20737 11493 41083 91687 37854 40379 86033 68448
47205 27292 48390 75786 66178 05529 41415 71193 66603 08189
28819 36678 77414 82317 80172 81269 34985 73578 32709 50758
57659 19749 47039 19315 29675 96669 23404 88030 23624 47049
10353 17809 08226 11674 69507 74641 91287 72824 43305 83239
50925 25499 35509 25261 68572 45956 57413 17934 41675 01485
02425 95069 50647 38395 65747 91365 19351 79833 45353 62521
43003 54012 60267 71622 67216 04198 10652 26316 93551 88780
38814 48314 06525 26168 78509 55526 46051 07117 20009 97092
91249 54437 88874 96062 88291 17250 63001 30362 29349 16080
25459 46149 45788 71427 83235 08292 42102 09182 58967 53560
43086 99380 16892 49889 26809 95101 69055 91995 11950 27887
17830 83701 83402 36474 54888 22221 61573 22801 01329 74509
27344 59450 43433 00901 09692 80253 52751 83328 98844 61508
94042 48265 01819 38515 62535 79639 96189 93967 90549 66380
03222 34872 39670 18485 18643 90591 04575 62726 24641 95387.

前 n 位数字

当前学术界尚无法计算葛立恒数在十进制下的首位数字（且很可能永远无法实现），但可确定：

• 二进制下首位必为 1（因所有非零正整数均满足此性质）
• 三进制下首位必为 1（因其是 3 的幂）
• 九进制下首位必为 3（因其是 3 的奇数次幂）

除非进制本身是 3 的幂（如 27 进制），或与葛立恒数可比（如葛立恒数减 64），否则无法计算其在其他进制下的首位数字。

不过，仍然可以进行概率估计：葛立恒数以$d$为开头的概率为

$P_d={\log }_{10}(d+1)-{\log }_{10}(d)={\log }_{10}(1+\frac{1}{d})$

如以 $123$ 为开头的概率就是 $P_{123}={\log }_{10}(1+\frac{1}{123})\approx 0.0035$