Kirby-Paris Hydra
更多操作
Kirby-Paris Hydra(KP Hydra)是在一棵树上进行的单人游戏,需要很长时间才能终止。[1]由此游戏导出的函数 的增长率超过了皮亚诺公理体系可证明停机的一切递归函数。它与 Beklemishev's worm 密切相关。
有序有根树
KP Hydra 的规则定义在有序有根树上,所以有必要简单了解有序有根树的概念.
正如“有序有根树”的名字所说,“有序有根树”有一个节点是树根(根节点),根节点下面挂着若干(有限)棵子树,每棵子树也是一个“有序有根树”.这些子树从左到右依次排列,不能交换顺序,这就是“有序”的含义。下图是两棵不同的有序有根树。
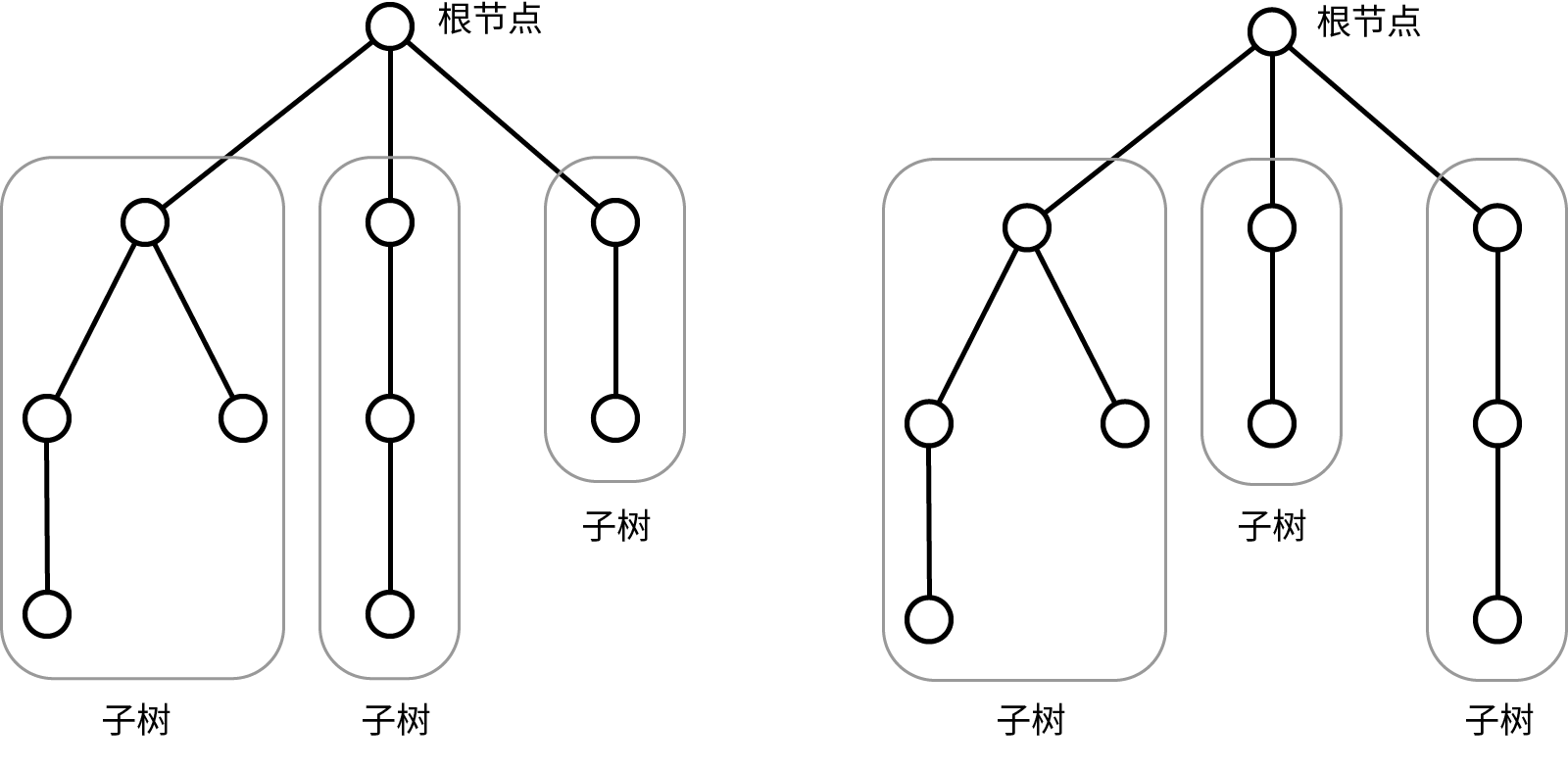
如果一个节点下面没有挂任何子树,那么称它是叶子节点。如果节点 在节点 下面且二者相邻,则称 是 的子节点, 是 的父节点。根节点不是任何节点的子节点。
如果一棵树里,除了叶子节点外,每个节点下只有一棵子树,则称这棵树是链状树。
规则
KP Hydra 游戏的规则如下:
- 游戏从一棵有 个节点的链状有序有根树 开始;
- 第 回合,选择 的最右边的叶子节点 ,设 的父节点为 ,依次执行以下操作(称为一次砍树):
- 删除 ;
- 若 不是根节点,取以 为根的子树 ,将其复制 次,连接到 的父节点上。
- 如果某步操作后只剩下根节点,游戏结束。
我们可以用括号表示树:每一对括号表示一个节点,最外层的括号表示根节点,每个括号内层的括号表示它的子节点。
例如:设 ,考虑这样的一棵树 。
将红色的括号删除后,树的变化如下:
以 为例,我们从一棵包含 4 个节点的链状有序有根树出发,进行第 1 次砍树:
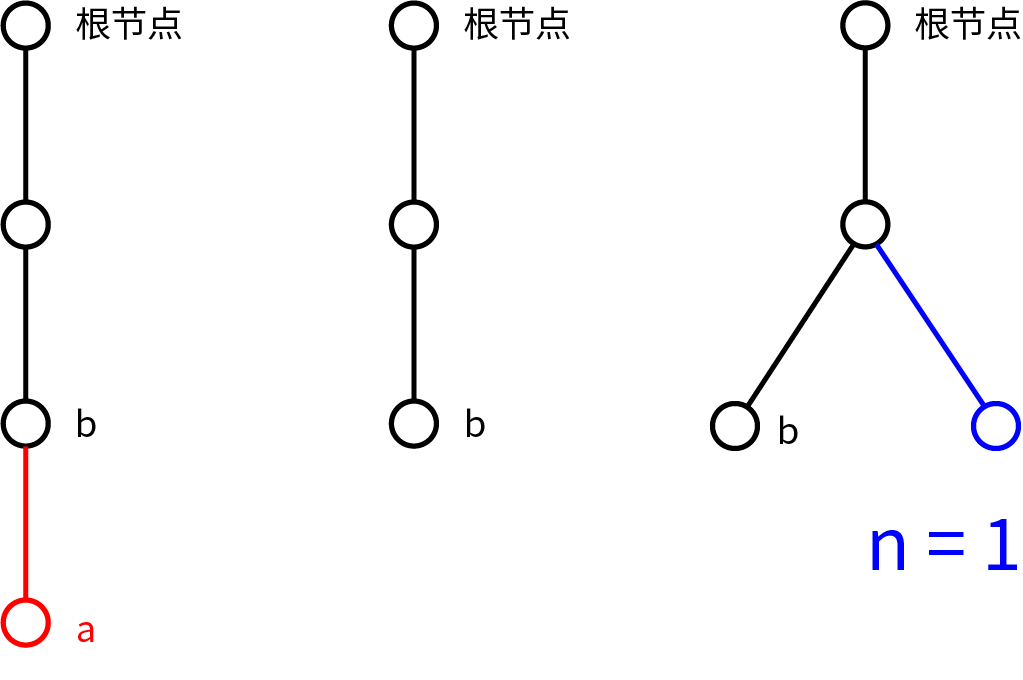
其中即将被删除的节点标为红色,新复制出来的节点标为蓝色.
第 2 次砍树:
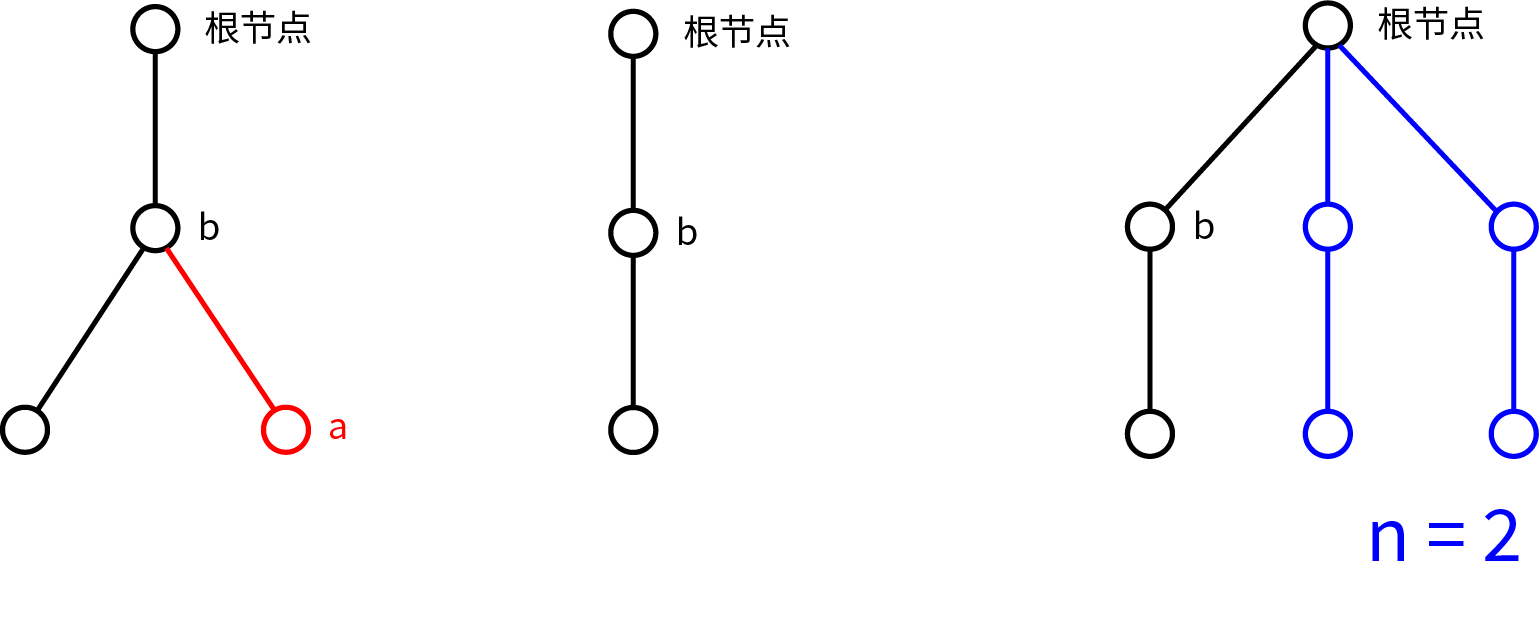
依此类推:
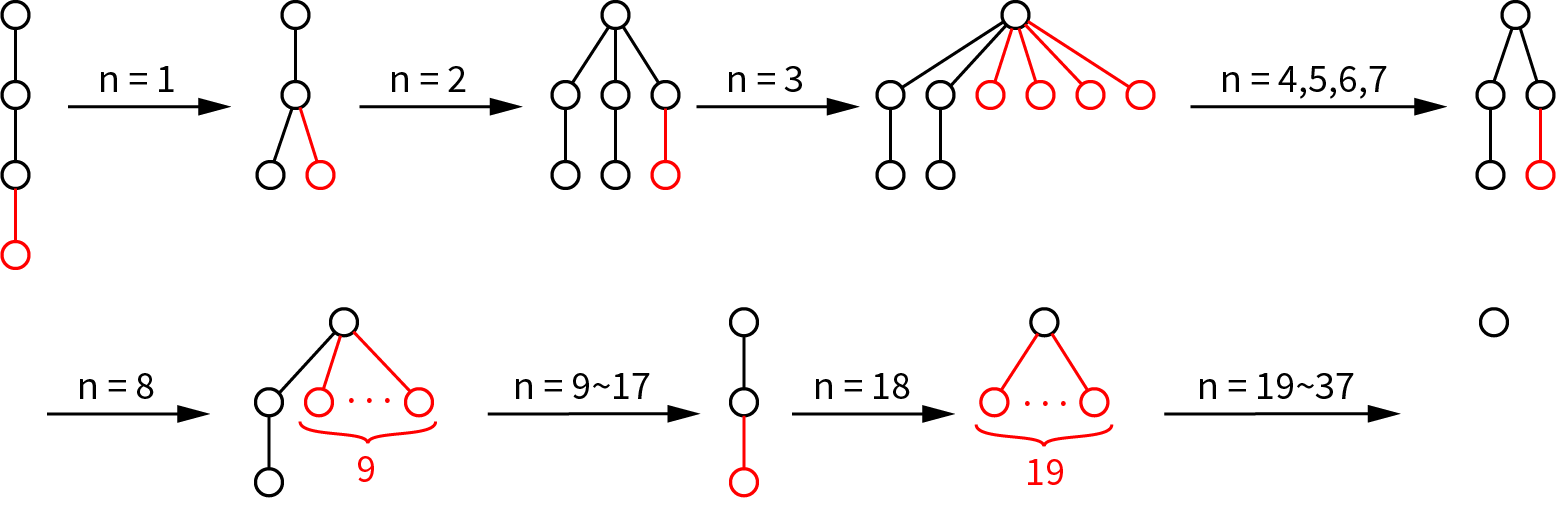
经过 37 次砍树,这棵树只剩一个节点,游戏结束.所以 .
停机性证明
Kirby 和 Paris 证明了以下定理:无论初始的树T怎样选取,KP Hydra 游戏总会在有限步内终止。
其证明概要如下:
我们给每个非空树对应一个序数:
- 只含根节点的树 对应 0
- 若树 分别对应序数 (通过重新排列,不妨设 ),则对应
例如,。
对树的深度归纳可知,每棵树对应的序数都小于 。
设初始的树为 。我们证明:砍树操作后,树对应的序数严格减小。
- 若选取节点的父节点为根节点,则 ,其对应的序数形如 ,砍树操作后变为 ,严格减小;
- 否则,设其父节点所在的子树为 ,其对应序数 。进行砍树操作后,该子树变为 ,对应序数 ,严格减小。
假设游戏从 开始可以无限地进行下去,我们可以得到一系列树 ,它们对应的序数满足 ,这与 的良序性矛盾。故游戏总会在有限步内终止。
Hydra 函数
我们用 表示以下特殊的 KP Hydra 游戏终止所需要的步数:[2]
- 初始树为含 个节点的链,即形如 的树;
- 每次操作总选取最右边的节点。
下面列出 较小时 的值:
其中为快速增长层级。一般地,记 ,其中有 个 ,则 。因此, 的增长率为 。
参考资料
- ↑ Kirby, L., & Paris, J. (1982). Accessible independence results for Peano arithmetic. Bulletin of the London Mathematical Society, 14: 285–293.
- ↑ Googology Wiki. Kirby-Paris Hydra. (EB/OL), Googology Wiki. https://googology.fandom.com/wiki/Kirby-Paris_hydra