葛立恒数:修订间差异
更多操作
无编辑摘要 |
无编辑摘要 |
||
| 第20行: | 第20行: | ||
葛立恒数源于拉姆齐理论中以下未解决的问题:<ref>Weisstein, Eric W. "Graham's Number." From ''MathWorld''--A Wolfram Resource. https://mathworld.wolfram.com/GrahamsNumber.html</ref> | 葛立恒数源于拉姆齐理论中以下未解决的问题:<ref>Weisstein, Eric W. "Graham's Number." From ''MathWorld''--A Wolfram Resource. https://mathworld.wolfram.com/GrahamsNumber.html</ref> | ||
设 <math>N</math> | 设 <math>N</math> 为超立方体的最小维度 <math>n</math>,使得对于任意 <math>n\geqslant N</math>,若将连接所有顶点对的线段用两种颜色着色,则必然存在一个单色的完全图 K₄(其顶点共面)。求N*的值。 | ||
[[文件:GrahamCube.png|缩略图|图中展示了一个立方体的示例,包含 12 个共面的 K₄ 完全图,其中下方显示了一个单色 K₄。若将该 K₄ 底部的边改为蓝色,则立方体中将不存在单色的共面 K₄,从而证明 <math>N^*</math> 至少为 4。]] | [[文件:GrahamCube.png|缩略图|图中展示了一个立方体的示例,包含 12 个共面的 K₄ 完全图,其中下方显示了一个单色 K₄。若将该 K₄ 底部的边改为蓝色,则立方体中将不存在单色的共面 K₄,从而证明 <math>N^*</math> 至少为 4。]] | ||
为理解问题,首先考虑任意维度的超立方体(1维为线段,2维为正方形,3维为立方体,4维为超立方体等),记其维度为 <math>N</math>。然后想象将所有顶点对用线段连接,并用红色或蓝色为每条线段着色(右侧展示了3维立方体的一种着色方式)。问题要求找到最小的维度 <math>N</math>,使得所有可能的着色方式中必然存在一个单色的完全图 K₄(由四个两两相连的顶点构成,且所有边颜色相同)。 | 为理解问题,首先考虑任意维度的超立方体(1维为线段,2维为正方形,3维为立方体,4维为超立方体等),记其维度为 <math>N</math>。然后想象将所有顶点对用线段连接,并用红色或蓝色为每条线段着色(右侧展示了3维立方体的一种着色方式)。问题要求找到最小的维度 <math>N</math>,使得所有可能的着色方式中必然存在一个单色的完全图 K₄(由四个两两相连的顶点构成,且所有边颜色相同)。 | ||
1971 年,R.L.Graham | 1971 年,R.L.Graham, B.L.Rothschild 在他们的论文<ref>GRAHAM R L, ROTHSCHILD B L. Ramsey’s theorem for $n$-parameter sets[J]. Transactions of the American Mathematical Society, 1971, 159: 257-292. https://www.ams.org/journals/tran/1971-159-00/S0002-9947-1971-0284352-8/S0002-9947-1971-0284352-8.pdf</ref>中为葛立恒问题提供的上界是 <math>F(F(F(F(F(F(F(12,3),3),3),3),3),3),3)</math>,其中 <math>F</math> 函数的定义为: <math>F(m,n)=\begin{cases}F(m-1,F(m,n-1))&,m\geqslant1\text{ and }n\geqslant2\\2^n&,m=1\\4&,n=2\end{cases}</math>,这相当于 <math>F^7(12)</math> 其中 <math>F(n)=2\uparrow^n3</math>。Sbiis Saibian 称这个数字为 “Little Graham”。 | ||
1976 年,Donald E.Knuth 在他的论文<ref>Donald E. Knuth, ''Mathematics and Computer Science: Coping with Finiteness'', Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations, Science 194, pp. 1235--1242, 1976.https://cse-robotics.engr.tamu.edu/dshell/cs625/finiteness.pdf</ref>中定义了现在所使用的高德纳箭头。 | 1976 年,Donald E.Knuth 在他的论文<ref>Donald E. Knuth, ''Mathematics and Computer Science: Coping with Finiteness'', Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations, Science 194, pp. 1235--1242, 1976.https://cse-robotics.engr.tamu.edu/dshell/cs625/finiteness.pdf</ref>中定义了现在所使用的高德纳箭头。 | ||
| 第30行: | 第30行: | ||
1977 年,M.Gardner 在他的文章<ref>GARDNER M. Mathematical games[J]. Scientific American, 1977, 237(3): 28-38.https://raw.githubusercontent.com/AllenDowney/ModSimPy/master/papers/scientific_american_nov_77.pdf</ref>中定义了现在的葛立恒数。Gardner 在发现这个数字的大小时,发现很难解释,他设计了一个更大、更容易解释的数字,格雷厄姆在 1977 年一篇未发表的论文中证明了这一点。他在 Scintific Amercian 上写了关于这个数字的文章,它甚至在 1980 年作为数学证明中使用的最大数字进入吉尼斯世界纪录,尽管几年后该称号从吉尼斯世界纪录中删除。一说是 Gardner 在与 Graham 交流后,Graham 给他提供的这个较为宽松的上界,但无从考证,Gardner 的原文章里也没有提及此事。 | 1977 年,M.Gardner 在他的文章<ref>GARDNER M. Mathematical games[J]. Scientific American, 1977, 237(3): 28-38.https://raw.githubusercontent.com/AllenDowney/ModSimPy/master/papers/scientific_american_nov_77.pdf</ref>中定义了现在的葛立恒数。Gardner 在发现这个数字的大小时,发现很难解释,他设计了一个更大、更容易解释的数字,格雷厄姆在 1977 年一篇未发表的论文中证明了这一点。他在 Scintific Amercian 上写了关于这个数字的文章,它甚至在 1980 年作为数学证明中使用的最大数字进入吉尼斯世界纪录,尽管几年后该称号从吉尼斯世界纪录中删除。一说是 Gardner 在与 Graham 交流后,Graham 给他提供的这个较为宽松的上界,但无从考证,Gardner 的原文章里也没有提及此事。 | ||
1995 年,John.H.Conway | 1995 年,John.H.Conway, Richard.K.Guy 在 The Book of Numbers 一书<ref>Conway, J. H., & Guy, R. K. (1995). The Book of Numbers. Copernicus. https://studylib.net/doc/26253636/the-book-of-numbers</ref>中给出了葛立恒数,这被许多人认为是它的来源。 | ||
2013 | 2003 年,Exoo <ref>Exoo, . A Euclidean Ramsey Problem . ''Discrete Comput Geom'' 29, 223–227 (2003). https://doi.org/10.1007/s00454-002-0780-5</ref><ref>Exoo, G. "A Ramsay Problem on Hypercubes." http://isu.indstate.edu/ge/GEOMETRY/cubes.html</ref>证明了 <math>N^*\geqslant11</math>。 | ||
2008 年,Jerome Barkley <ref>http://arxiv.org/abs/0811.1055</ref>证明了 <math>N^*\geqslant13</math>。 | |||
2013 年,Mikhail Lavrov, Mitchell Lee, John Mackey <ref>http://arxiv.org/abs/1304.6910</ref>通过使用 Hales-Jewett 定理将上限进一步降低到 <math>N^*=2\uparrow\uparrow2\uparrow\uparrow(3+2\uparrow\uparrow8)</math>。 | |||
2019 年,Eryk Lipka <ref>http://arxiv.org/abs/1905.05617</ref>将上限进一步降低到 <math>(2\uparrow\uparrow5138)\times((2\uparrow\uparrow5140)\uparrow\uparrow(2\times2\uparrow\uparrow5137))\ll2\uparrow\uparrow\uparrow5</math>。 | |||
=== 比较 === | |||
==== 计算最后位数 ==== | |||
可通过简单的模幂算法轻松计算葛立恒数的最后位数。以下是一个获取较小 x 值对应葛立恒数末 x 位数 N(x) 的简易算法: | |||
<math>N(x)=\begin{cases}3&,x=0\\3^{N(x-1)}\pmod{10^x}&,x\neq0\end{cases}</math> | |||
然而,若将该公式应用于极大的x值则不成立——尽管该错误公式曾被认为正确,并在 2019 年 12 月前于英语 googology 社区流传。可通过以下思路修正错误:葛立恒数 G(64) 实质是以 3 为底、以极大值 b 为超指数的整数迭代幂次(即 <math>G(64)={}^b3</math> )。 | |||
2020年,Marco Ripà 证明<ref>Ripà, M. (2020). On the constant congruence speed of tetration. Notes on Number Theory and Discrete Mathematics, 26 (3), 245-260, DOI: 10.7546/nntdm.2020.26.3.245-260. https://nntdm.net/volume-26-2020/number-3/245-260/</ref><ref>Ripà, M., & Onnis, L. (2022). Number of stable digits of any integer tetration. Notes on Number Theory and Discrete Mathematics, 28(3), 441-457, DOI: 10.7546/nntdm.2022.28.3.441-457. https://nntdm.net/volume-28-2022/number-3/441-457/</ref>了在十进制下,当且仅当超指数为 1 时 3 的 congruence speed(同余速度)为 0,否则恒为 1。因此,对所有 <math>c=1,2,\cdots,b-2,b-1</math>, G(64) 的末 b-1 位数与 <math>{}^c3</math> 相同。但此性质不适用于 G(64) 的第 b 位数——该数字与 <math>{}^{b+1}3,{}^{b+2}3,{}^{b+3}3,\cdots</math> 的第 b 位数均不相等。由 <math>b-1=\text{slog}_3(G_{64})-1</math>(其中 slog 表示超对数)可得 <math>G_{63} \ll b-1 \ll G_{64}</math>。故最终可证:对所有正整数 c ,满足: | |||
<math>G_{64}\equiv{^{slog_3(G_{64})+c}}3\pmod{{10}^{slog_3(G_{64})-1}}\land G_{64}\not\equiv{^{slog_3(G_{64})+c}}3\pmod{{10}^{slog_3(G_{64})}}</math> | |||
实际上,该方法会返回映射 <math>x \mapsto 3^x</math> 在 10 进制整数中的不动点的最后位数。因此上述“错误算法”仅能计算葛立恒数的末 b-1 位。由于 b 值极大(在此尺度下几乎与葛立恒数本身相当),该算法对所有实际应用的 x 值均有效——这可能是其曾被推广至任意正整数 x 的原因。 | |||
葛立恒数的末 20 位是:...04,575,627,262,464,195,387。 | |||
当前学术界尚无法计算葛立恒数在十进制下的首位数字(且很可能永远无法实现),但可确定: | |||
* 二进制下首位必为1(因所有非零正整数均满足此性质) | |||
* 三进制下首位必为1(因其是3的幂) | |||
* 九进制下首位必为3(因其是3的奇数次幂) | |||
除非进制本身是3的幂(如27进制),或与葛立恒数可比(如葛立恒数减64),否则无法计算其在其他进制下的首位数字。 | |||
=== 参考资料 === | === 参考资料 === | ||
2025年7月2日 (三) 10:25的版本
葛立恒数(Graham's Number)是拉姆齐理论中一个问题(即葛立恒问题)的上界。它也是大数领域中最著名的数之一,与TREE(3)、SCG(3)齐名。
定义
葛立恒函数
葛立恒函数(Graham's Function)是用高德纳箭头递归定义的:
葛立恒数
葛立恒数被定义为 (有时也被写作 等)。
更出名的一个写法是:
历史
葛立恒数源于拉姆齐理论中以下未解决的问题:[1]
设 为超立方体的最小维度 ,使得对于任意 ,若将连接所有顶点对的线段用两种颜色着色,则必然存在一个单色的完全图 K₄(其顶点共面)。求N*的值。
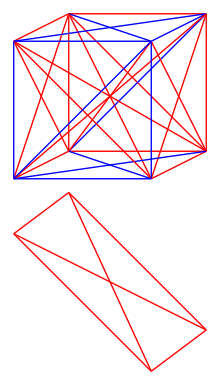
为理解问题,首先考虑任意维度的超立方体(1维为线段,2维为正方形,3维为立方体,4维为超立方体等),记其维度为 。然后想象将所有顶点对用线段连接,并用红色或蓝色为每条线段着色(右侧展示了3维立方体的一种着色方式)。问题要求找到最小的维度 ,使得所有可能的着色方式中必然存在一个单色的完全图 K₄(由四个两两相连的顶点构成,且所有边颜色相同)。
1971 年,R.L.Graham, B.L.Rothschild 在他们的论文[2]中为葛立恒问题提供的上界是 ,其中 函数的定义为: ,这相当于 其中 。Sbiis Saibian 称这个数字为 “Little Graham”。
1976 年,Donald E.Knuth 在他的论文[3]中定义了现在所使用的高德纳箭头。
1977 年,M.Gardner 在他的文章[4]中定义了现在的葛立恒数。Gardner 在发现这个数字的大小时,发现很难解释,他设计了一个更大、更容易解释的数字,格雷厄姆在 1977 年一篇未发表的论文中证明了这一点。他在 Scintific Amercian 上写了关于这个数字的文章,它甚至在 1980 年作为数学证明中使用的最大数字进入吉尼斯世界纪录,尽管几年后该称号从吉尼斯世界纪录中删除。一说是 Gardner 在与 Graham 交流后,Graham 给他提供的这个较为宽松的上界,但无从考证,Gardner 的原文章里也没有提及此事。
1995 年,John.H.Conway, Richard.K.Guy 在 The Book of Numbers 一书[5]中给出了葛立恒数,这被许多人认为是它的来源。
2008 年,Jerome Barkley [8]证明了 。
2013 年,Mikhail Lavrov, Mitchell Lee, John Mackey [9]通过使用 Hales-Jewett 定理将上限进一步降低到 。
2019 年,Eryk Lipka [10]将上限进一步降低到 。
比较
计算最后位数
可通过简单的模幂算法轻松计算葛立恒数的最后位数。以下是一个获取较小 x 值对应葛立恒数末 x 位数 N(x) 的简易算法:
然而,若将该公式应用于极大的x值则不成立——尽管该错误公式曾被认为正确,并在 2019 年 12 月前于英语 googology 社区流传。可通过以下思路修正错误:葛立恒数 G(64) 实质是以 3 为底、以极大值 b 为超指数的整数迭代幂次(即 )。
2020年,Marco Ripà 证明[11][12]了在十进制下,当且仅当超指数为 1 时 3 的 congruence speed(同余速度)为 0,否则恒为 1。因此,对所有 , G(64) 的末 b-1 位数与 相同。但此性质不适用于 G(64) 的第 b 位数——该数字与 的第 b 位数均不相等。由 (其中 slog 表示超对数)可得 。故最终可证:对所有正整数 c ,满足:
实际上,该方法会返回映射 在 10 进制整数中的不动点的最后位数。因此上述“错误算法”仅能计算葛立恒数的末 b-1 位。由于 b 值极大(在此尺度下几乎与葛立恒数本身相当),该算法对所有实际应用的 x 值均有效——这可能是其曾被推广至任意正整数 x 的原因。
葛立恒数的末 20 位是:...04,575,627,262,464,195,387。
当前学术界尚无法计算葛立恒数在十进制下的首位数字(且很可能永远无法实现),但可确定:
- 二进制下首位必为1(因所有非零正整数均满足此性质)
- 三进制下首位必为1(因其是3的幂)
- 九进制下首位必为3(因其是3的奇数次幂)
除非进制本身是3的幂(如27进制),或与葛立恒数可比(如葛立恒数减64),否则无法计算其在其他进制下的首位数字。
参考资料
- ↑ Weisstein, Eric W. "Graham's Number." From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/GrahamsNumber.html
- ↑ GRAHAM R L, ROTHSCHILD B L. Ramsey’s theorem for $n$-parameter sets[J]. Transactions of the American Mathematical Society, 1971, 159: 257-292. https://www.ams.org/journals/tran/1971-159-00/S0002-9947-1971-0284352-8/S0002-9947-1971-0284352-8.pdf
- ↑ Donald E. Knuth, Mathematics and Computer Science: Coping with Finiteness, Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations, Science 194, pp. 1235--1242, 1976.https://cse-robotics.engr.tamu.edu/dshell/cs625/finiteness.pdf
- ↑ GARDNER M. Mathematical games[J]. Scientific American, 1977, 237(3): 28-38.https://raw.githubusercontent.com/AllenDowney/ModSimPy/master/papers/scientific_american_nov_77.pdf
- ↑ Conway, J. H., & Guy, R. K. (1995). The Book of Numbers. Copernicus. https://studylib.net/doc/26253636/the-book-of-numbers
- ↑ Exoo, . A Euclidean Ramsey Problem . Discrete Comput Geom 29, 223–227 (2003). https://doi.org/10.1007/s00454-002-0780-5
- ↑ Exoo, G. "A Ramsay Problem on Hypercubes." http://isu.indstate.edu/ge/GEOMETRY/cubes.html
- ↑ http://arxiv.org/abs/0811.1055
- ↑ http://arxiv.org/abs/1304.6910
- ↑ http://arxiv.org/abs/1905.05617
- ↑ Ripà, M. (2020). On the constant congruence speed of tetration. Notes on Number Theory and Discrete Mathematics, 26 (3), 245-260, DOI: 10.7546/nntdm.2020.26.3.245-260. https://nntdm.net/volume-26-2020/number-3/245-260/
- ↑ Ripà, M., & Onnis, L. (2022). Number of stable digits of any integer tetration. Notes on Number Theory and Discrete Mathematics, 28(3), 441-457, DOI: 10.7546/nntdm.2022.28.3.441-457. https://nntdm.net/volume-28-2022/number-3/441-457/