ω-Y:修订间差异
更多操作
Apocalypse(留言 | 贡献) 无编辑摘要 |
小无编辑摘要 |
||
| (未显示3个用户的6个中间版本) | |||
| 第1行: | 第1行: | ||
ω-Y,是一种 [[Beklemishev's Worm|Worm]] 型序数记号。 | |||
== 定义 == | === 定义 === | ||
=== 合法表达式 === | ==== 合法表达式 ==== | ||
一个合法的 | 一个合法的 ω-Y 表达式是以 1 开头的正整数序列,即形如 | ||
<math>(a_1,a_2,\cdots,a_n)\quad(n,a_1,a_2,\cdots,a_n\in\N,a_1=1)</math> | <math>(a_1,a_2,\cdots,a_n)\quad(n,a_1,a_2,\cdots,a_n\in\N,a_1=1)</math> | ||
| 第10行: | 第10行: | ||
的序列。 | 的序列。 | ||
例如:<math>(1,4,6,4)</math> | 例如:<math>(1,4,6,4)</math> 以及 <math>(1,1,4,5,1,4)</math> <s>''这样的果糕''</s>都是合法的 ω-Y 表达式,而 <math>(1,2,\pi)</math> 不是。 | ||
=== | ==== 山脉图 ==== | ||
要描述 ω-Y 的展开规则或者直观理解部分定义,需要用到'''山脉图'''的辅助。 | |||
'''行标'''可以说是 ω-Y,以及后续可能的 α-Y 扩展当中,最为重要的概念,没有之一。它是各种复杂的 Y 系列序列的运行基础。 | |||
在 ω-Y 中,每一行的行标都是 <math>\omega^\omega</math> 以下,0 以上的序数。我们采用不同等级的分隔线对行标进行划分。具体地,0 级分隔线(也就是什么都没有)表示它上面的行的行标等于下面的行的行标 ;1 级分隔线(普通的单横线)表示 它上面的行的行标等于下面的行的行标+ω;2 级分隔线(双重横线)表示它上面的行的行标等于下面的行的行标+ω<sup>2</sup>;以此类推,n 级分隔线(n 重横线)表示它上面的行的行标等于下面的行的行标+ω<sup>n</sup>。 | |||
图 1 是一个较为复杂的山脉图对应的行标的例子。 | |||
[[文件:v2-f079776a0fd9225aa0a8a52765ed8ba9 1440w.png|缩略图|582x582像素|Fig.1 山脉图]] | |||
ω-Y 的山脉图中,父项、左腿、右腿、阶差等含义与 [[0-Y]]、[[Y序列|1-Y]] 完全一致,这里不做重复介绍。 | |||
一般来说,ω-Y 的山脉图具有以下特点: | |||
= | # 不进行提取操作。提取操作的目的可以说是让“本来找不到父项的项”有机会与其它项位于同一行,从而可以找到父项。而在标准的 ω-Y 表达式之中,所有大于 1 的项都可以按规则找到父项。因此,无需进行提取。 | ||
# 每一列最顶端的数都是 1。这个特点可以由上一条推理得到。既然每个大于 1 的项都存在父项,那么它和父项之间就会有阶差,而阶差位于这一项的上方。也就是说,只要一个数不是 1,那么它的上面就还会有别的数字。因此,每一列最上方都是 1。反过来,所有的 1 都一定位于所在列的顶端。这一条特点可以作为一个 ω-Y 山脉图是否完整的验证方式。 | |||
# 某一项、它的父项、以及它和父项之间的阶差项的行标关系。假设这一项的行标为β,其父项的行标为α,那么: (1) <math>\alpha=\beta</math> 时:阶差项的行标为 <math>\beta+1</math>。也就是说,如果该项和父项位于同一行,那么阶差项在它们上面一行,中间相隔一条 0 级分隔线(nothing)。 (2) <math>\alpha+1\leq\beta<\alpha+\omega</math> 时:阶差项的行标为 <math>\beta+\omega</math>。也就是说,如果该项和父项不位于同一行,但之间只有 0 级分隔线,那么阶差项在它们上面 <math>\omega</math> 行,中间相隔一条 1 级分隔线。 (3) <math>\alpha+\omega^n\leq\beta<\alpha+\omega^{n+1}</math> 时:阶差项的行标为 <math>\beta+\omega^{n+1}</math>。也就是说,如果该项和父项之间的分隔线等级最高为 n 的话,那么阶差项在它们上面 <math>\omega^{n+1}</math> 行,中间相隔一条 n+1 级分隔线。 | |||
接下来是通过山脉图找到父项的方法。为了更好地解释找父项的行为,我们需要引入待定父项这一重要概念。值得一提的是,对于具备一定复杂度的记号,“通过待定父项来确定父项”几乎都成为了必不可少的一步。所以,了解这一概念以及它的相关运作方式,不止对 ω-Y 的理解有帮助。 | |||
具体地,对于 ω-Y 山脉图中的某一项(记作 X),我们从 X 出发,沿左腿向左下走一步,然后沿右腿向上一直走到行标至多为 X 的行标的位置(有可能一步都走不了),最后停留的位置就是 X 的待定父项。 | |||
在 {X, X的待定父项, X的待定父项的待定父项, ...} 形成的序列中,最先遇到的数值小于 X 的项即为 X 的父项。我们算出 X 与其父项的阶差,根据这两项的位置按照上面的规律确定阶差项的位置,然后画出阶差项的左腿和右腿。不断对每一个新生成的项重复这一过程,直到无法这样做,最终就能得到完整的 ω-Y 山脉图。 | |||
[https://naruyoko.github.io/MEGAwhYmountain MEGAwhY mountain] 可以绘制 ω-Y 的山脉图。 | |||
==== 展开 ==== | |||
概念介绍: | |||
为了更好地介绍 ω-Y 的展开,我们又不得不又引入一些新的概念以及对 1-Y 中的概念做出一些修正: | |||
'''根元素、根列''':山脉图的最右列最上方元素所连接的左腿所指的元素,称为根元素。其所在的列为根列。 | |||
'''根列元素''':位于根列的、行标小于等于根元素行标的元素,称为根列元素。 | |||
'''作用区域''':假设所有根列元素的行标从小到大依次为 <math>\alpha_0,\alpha_1,\cdots,\alpha_n</math>,那么对于行标为 <math>\alpha_k,k\leq n</math> 的元素,其作用区域为根列(含)向右、行标从 <math>\alpha_k</math>(含元素,不含其下方的边)到 <math>\alpha_{k+1}</math>(不含元素,含其下方的边)的区域。<math>\alpha_{n+1}</math> 被规定为山脉最右列最上方元素所在的行标。每一个根列元素都与一块作用区域一一对应,并且这些作用区域相互不重叠。 | |||
'''轮廓边''':从一个根列元素出发,沿左腿向上一步(但不能超出这个根列元素的作用区域)之后,沿右腿向下若干步(可以不向下,但同样不能超出这个根列元素的作用区域),随后重复这个过程直到无路可走。能通过这样的操作经过的边,都是这个根列元素对应的(或者这个作用区域内的)移动边。这些边的特点是,复制时左右腿连接的对象均会移动。 | |||
'''非轮廓边''':经过了某个作用区域,但不符合这个作用区域内轮廓边的概念的边,称为这个作用区域内的固定边。这些边的特点是,复制时左腿连接的对象保持不变。 | |||
'''填充边''':从一个根列元素出发,沿左腿向上走一行后,沿右腿向下走一行,随后重复这个过程直到无路可走。能通过这样的操作经过的边,称为这个根列元素对应的填充边。填充边属于移动边。 | |||
'''行差''':在本文,我们约定第 <math>\alpha</math> 行和第 <math>\beta</math> 行(<math>\alpha\leq\beta</math>)的行差为满足 <math>\alpha+\delta=\beta</math> 的序数 <math>\delta</math>。例如,第 <math>\omega</math> 行和第 <math>\omega^2</math> 行的行差为 <math>\omega^2</math>,第 <math>\omega+1</math> 行和第 <math>\omega\times2+1</math> 行的行差为 <math>\omega+1</math>。 | |||
一个根列元素,对应了一块作用区域、一组轮廓边和一组填充边。 | |||
展开规则: | |||
在展开ω-Y时,我们先将末列减一,然后从上到下依次处理每一个作用区域。对于每一个作用区域,我们依次进行以下操作: | |||
'''轮廓边的复制:'''我们将轮廓边的端点及其所指的元素向右上方进行复制。具体地,向右平移(末列位置-根列位置)的列数,然后向上平移至满足以下条件的位置:若平移前端点所指的元素与根列元素行差为<math>\delta_0</math>,那么平移后对应端点所指的元素与末列最上方的元素行差也要为<math>\delta_0</math>。像这样,直至所有的轮廓边和它们所指的元素都被复制到了新的位置上。 | |||
'''填充边的复制:'''如果上一步中中,末列最上方元素与根列元素的行差为0,那么无需复制填充边,直接跳过这一步。否则,需要将轮廓边向上移动所造成的空位使用填充边进行填补。具体的做法与1-Y的填充是类似的,但从上向下进行,并且需要处理填补极限序数行时,左右脚的行差问题。 | |||
'''非轮廓边的复制''' | |||
这些边的复制最后进行。它们的左腿指向的元素都保持不动,而右腿向右或右上平移。向右平移的列数依旧是(末列位置-根列位置)。如果这条非轮廓边右腿所指元素没有被这个作用区域内的轮廓边所指到,那么无需向上平移;如果有,那么向上平移到与末列最上方元素行差为<math>\delta_0</math>的位置。这里的<math>\delta_0</math>依旧是平移之前该元素与根列元素的行差。 | |||
重复这三步的操作(注意每次操作时末列的位置和作用区域内末列最上方元素的行标会变化),我们便能得到指定ω-Y表达式的基本列。 | |||
==== 运算实例 ==== | |||
ω-Y(1,3,10,29,36) 的展开:首先,画出 ω-Y(1,3,10,29,36) 的山脉图,如图 2: | |||
[[文件:v2-7ad73bd4607b624ec3a52b8dc244eff2 1440w.png|居中|缩略图|333x333像素|Fig.2 ω-Y(1,3,10,29,36) 的山脉图]] | |||
显然,根列是第二列,根元素为第二列第 <math>\omega</math> 行的 1。因此,这个山脉图中有三个根列元素,需要划分出三个作用区域,如图 3 所示。 | |||
[[文件:v2-9385a2a9af6930cf91ff7f828eac33f8 1440w.png|居中|缩略图|Fig.3 ω-Y(1,3,10,29,36) 的作用区域]] | |||
接着,我们就按照前面所说的,将末列减一之后,开始从上到下依次处理每一个区域。 | |||
对最上方作用区域的处理,首先是对轮廓边进行复制。这一区域内的所有边都是轮廓边,根列元素行标为 <math>\omega</math>,末列最上方元素行标为 <math>\omega+1</math>。为了保持行差关系,我们把原来位于 <math>\omega</math> 行的元素随着复制平移到 <math>\omega+1,\omega+2,\cdots</math> 行,把原来位于 <math>\omega+1</math> 行的元素随着复制平移到 <math>\omega+1,\omega+2,\cdots</math> 行,如图 4 所示: | |||
[[文件:v2-2efd45a7d16156df97fd1c65a4e29508 1440w.png|居中|缩略图|Fig.4 ω-Y(1,3,10,29,36) 第一个作用区域的轮廓边复制情况]] | |||
这样一个简单的平移就完成了。注意,无论何时,作用区域内的东西都不会因为平移被移动到作用区域外。 | |||
紧接着进行填充边的复制和填充。我们找到填充边(图5深蓝色),并把它们向右和向右上填补到上一步生成的空隙中去(图5浅蓝色),就像这样: | |||
[[文件:v2-d274d65881b123f33bd817775f665035 1440w.png|居中|缩略图|Fig.5 ω-Y(1,3,10,29,36) 第一个作用区域的填充边复制情况]] | |||
和1-Y中的操作是一样的。毕竟,ω-Y(1,3,10,29,35)还没有超出1-Y极限。 | |||
最后是非轮廓边的复制。幸运的是,这一区域不存在非轮廓边,所以我们已经处理完成这一区域了。 | |||
对中间的作用区域的处理,还是先对轮廓边进行复制。这一个区域内,仍然所有的边都是轮廓边,根列元素行标为2,末列最上方元素行标为3,因此,我们所需要进行的平移操作和上面是一样的,找到填充边,把空隙填进去,和第一个区域一样。 | |||
[[文件:v2-615639380114bd7273910362ccddf7d9 1440w.png|居中|缩略图|Fig.6 ω-Y(1,3,10,29,36) 第二个作用区域的填充边复制情况]] | |||
第二个区域依然没有非轮廓边,那么这个区域也结束了。 | |||
最下方的区域只有一行,因此不会产生空隙,也就无需搭理填充边。所以,对它的处理也是最简单的。 | |||
[[文件:v2-3a6578e28b37fa97aba679bf84e3a26b 1440w.png|居中|缩略图|Fig.7 ω-Y(1,3,10,29,36) 的展开结果]] | |||
ω-Y(1,4,18,48,32) 的展开:首先,画出山脉图,并标出其中的根列元素、作用区域如下: | |||
[[文件:v2-ce2f495dd488ec1b1d4c10af94d4daca 1440w.png|居中|缩略图|Fig.8 ω-Y(1,4,18,48,32) 的根列元素和作用区域]] | |||
那么,依旧是把最右列减一,然后从上往下处理每一个根列元素。 | |||
== | 对最上方作用区域的处理,这个作用区域只有一行。那么是比较简单的,向右平移就好了。 | ||
[[文件:v2-74c51b23be596c00bce9f69523a13e1b 1440w.png|居中|缩略图|Fig.9 ω-Y(1,4,18,48,32) 第一个作用区域的轮廓边和填充边复制情况]] | |||
对第二个作用区域的处理,这个作用区域就有些复杂了。不过我们还是按照步骤,先找出所有的轮廓边如下: | |||
[[文件:v2-f46edbe81ca6fd2eb6917380eea3af10 1440w.png|居中|缩略图|Fig.10 ω-Y(1,4,18,48,32) 第二个作用区域的移动边]] | |||
可见,这个作用区域内的根列元素位于第 <math>\omega</math> 行,最右列的最上端元素位于第 <math>\omega\times2</math> 行。依照相对行差进行平移,我们把原来位于 <math>\omega</math> 行的元素随着复制平移到 <math>\omega\times2,\omega\times3,\cdots</math> 行,把原来位于 <math>\omega\times2</math> 行的元素随着复制平移到 <math>\omega\times3,\omega\times4,\cdots</math> 行,把原来位于 <math>\omega+1</math> 行的元素随着复制平移到 <math>\omega\times2+1,\omega\times3+1,\cdots</math> 行,如图 11 所示。 | |||
[[文件:v2-72c6d9583fcc6dbb6e25713096a7da61 1440w.png|居中|缩略图|Fig.11 ω-Y(1,4,18,48,32) 第二个作用区域的轮廓边复制情况]] | |||
现在,轮廓边复制完成了,轮到填充边。当空隙有多行时,填充边从上往下进行填充。但是,此时出现了一个特殊情况:我们需要把填充边复制到一个跨过了高级(≥1级)分隔线的位置上。为了确保山脉图的行标规则不被破坏,我们规定:当填充边被复制到跨过了 n 级分隔线的位置上时,其左腿和右腿的行差需要为 <math>\omega^{n-1}</math>。按照这个规定,我们先填充红色部分空隙的最上面一行,这样,就多出了一个 <math>\omega+2</math> 行。继续从上往下填充 <math>\omega+1</math> 行和 <math>\omega</math> 行的部分,以及按照同样流程完成橙色部分的填充,结束整个填充边复制的步骤。 | |||
[[文件:v2-9ff6998d06616808c1915a97bafd7244 1440w.png|居中|缩略图|Fig.12 ω-Y(1,4,18,48,32) 第二个作用区域的红色填充边复制情况]] | |||
[[文件:v2-b7590a7a2287b78f2a498878d2b5266e 1440w.png|居中|缩略图|Fig.13 ω-Y(1,4,18,48,32) 第二个作用区域的全部填充边复制情况]] | |||
但是第二个区域并没有处理完。在绿色的部分,有一条大黑边与其它的部分格格不入——它是非轮廓边。我们在最后需要对它进行处理。由于它右腿所指的元素并没有被轮廓边指到,所以直接向右平移,就像这样: | |||
[[文件:v2-8e9d38051032c086ddf932564b9f0201 1440w.png|居中|缩略图|Fig.14 ω-Y(1,4,18,48,32) 第二个作用区域的全部]] | |||
第三和第四个作用区域的复制,这两个区域的边的复制没有什么特殊的行为。 | |||
[[文件:v2-64eb9c30c422bd293219ef7ab76c499c 1440w.png|居中|缩略图|Fig.15 ω-Y(1,4,18,48,32) 第三个作用区域的轮廓边复制情况]] | |||
[[文件:v2-4335f18d3028aae51e7c6b73900ddfe0 1440w.png|居中|缩略图|Fig.16 ω-Y(1,4,18,48,32) 第三个作用区域的填充边和第四个区域复制情况]] | |||
于是我们完成了本例的展开。 | |||
=== n-Y 序列 === | |||
如果我们在 ω-Y 序列绘制山脉图的过程中绘制完 <math>\omega^{1+n}</math> 以下的部分就停止,则这样得到的序列就是 n-Y 序列。n-Y 序列的山脉图只有 <math>\omega^{1+n}</math>行,分隔山脉图的直线最多只有 n 重,它的展开规则与通常的 ω-Y 序列是一致的。n-Y 序列有两个不同的版本,其中 C n-Y (Consistent n−Y) 在绘制山脉图的过程中进行提取操作,而 D n-Y (Diagonlizing n−Y) 在绘制山脉图的过程中不进行提取操作。 | |||
对于 C n-Y 来说,我们有 <math>\text{C }n\text{-Y}(1,\omega)=\text{C }(n+1)\text{-Y}(1,3)</math> | |||
对于 D n-Y 来说,我们有 <math>\text{D }n\text{-Y}(1,\omega)=\text{D }(n+1)\text{-Y}(1,4)</math>,以及 <math>\text{D }n\text{-Y}(1,\omega)=\omega\text{-Y}(1,n+3)</math>。 | |||
=== Magma === | |||
以上介绍的 ω-Y 规则称为 weak magma 规则,它是目前最常用的规则。在未做说明的情况下,我们默认 ω −Y 的规则就是 weak magma 规则。除了 weak magma 规则之外,还有三种与之并列的规则,它们分别为 medium magma 规则,strong magma 规则以及 actual规则。在历史上,actual 规则是最先提出的,其余三种规则是之后提出的。而在现在看来,除了 weak magma 之外的三种规则基本已经被淘汰了,它们已经几乎只有历史上的意义了。 | |||
下面我们简要介绍上述四种规则的区别。我们引入 ω-Y 原版定义中的 magma 元素、wildfire 边、eruption 边以及 magma 边的概念(这与上面给出定义的顶点元素、参考边、轮廓边、平移边的概念并不完全相同)。每个根列元素都对应一组 magma 元素和 magma边,有两种不同的方法来对它们进行确定,分别为 weak magma 和 strong magma 两种规则。 | |||
# weak magma 的确定规则如下:从一个根列元素出发,沿左腿往右上方走一步(可能有多种走法),然后沿右腿向下走一步,如果到达了与根列元素同一行的复制部分,这个元素就是 magma 元素。从 magma 元素出发也(递归地)走同样的路。所有经过的边就是 magma 边。 | |||
# strong magma 的确定规则如下:从一个根列元素出发,沿右腿向下走一步,然后沿左腿往右上方走一步(可能有多种走法),如果到达了与根列元素同一行的复制部分,这个元素就是 magma 元素。从 magma 元素出发也(递归地)走同样的路。所有经过的边就是 magma 边。 | |||
作出新边的过程,可以分成 3 种不同的边,它们分别为 wildfire 边、eruption 边、magma边,这些边都是从复制部分复制出来的。其中,wildfire 边通常高度是不变的;eruption 边高度会提高,但数量仍与复制源相同;而 magma 边则会从一个复制源复制出许多份。而 weak magma 和 strong magma 两种规则在 magma 边的复制规则处又有所不同。 | |||
# weak magma 的复制规则如下:对每个 magma 元素,先沿右腿向上走一步,然后沿左腿向下一步,这个左腿就是我们接下来要复制的复制源。 | |||
# strong magma 的复制规则如下:对每个 magma 元素,直接沿左腿向下一步。这个左腿就是我们接下来要复制的复制源。 | |||
至此我们就可以区分出四种不同 ω-Y 的规则如下。 | |||
# weak magma ω − Y 的规则为:展开用的是 weak magma 规则,最初确定 magma 元素的时候用的也是 weak magma 规则。 | |||
# strong magma ω − Y 的规则为:展开用的是 strong magma 规则,最初确定 magma元素的时候用的也是 strong magma 规则。 | |||
# medium magma ω − Y 的规则为:展开用的是 strong magma 规则,最初确定 magma元素的时候用的是 weak magma 规则。 | |||
# actual ω − Y 的规则为:展开用的是 strong magma 规则;最初确定 magma 元素的时候,如果根列元素位于后继序数行(包括第 1 行)就用 strong magma 规则,否则用weak magma 规则。 | |||
这四种规则的 ω-Y 可以用 [https://hypcos.github.io/notation-explorer/ Notation Explorer] 展开。目前已知 weak、strong、medium 三种 magma 的 ω-Y 在 1,3,8 即 [[Catching|catch]]。 | |||
''主词条:[[ω-Y magma 对比分析]]''{{默认排序:序数记号}} | |||
[[分类:记号]] | [[分类:记号]] | ||
2025年8月24日 (日) 14:38的最新版本
ω-Y,是一种 Worm 型序数记号。
定义
合法表达式
一个合法的 ω-Y 表达式是以 1 开头的正整数序列,即形如
的序列。
例如: 以及 这样的果糕都是合法的 ω-Y 表达式,而 不是。
山脉图
要描述 ω-Y 的展开规则或者直观理解部分定义,需要用到山脉图的辅助。
行标可以说是 ω-Y,以及后续可能的 α-Y 扩展当中,最为重要的概念,没有之一。它是各种复杂的 Y 系列序列的运行基础。
在 ω-Y 中,每一行的行标都是 以下,0 以上的序数。我们采用不同等级的分隔线对行标进行划分。具体地,0 级分隔线(也就是什么都没有)表示它上面的行的行标等于下面的行的行标 ;1 级分隔线(普通的单横线)表示 它上面的行的行标等于下面的行的行标+ω;2 级分隔线(双重横线)表示它上面的行的行标等于下面的行的行标+ω2;以此类推,n 级分隔线(n 重横线)表示它上面的行的行标等于下面的行的行标+ωn。
图 1 是一个较为复杂的山脉图对应的行标的例子。
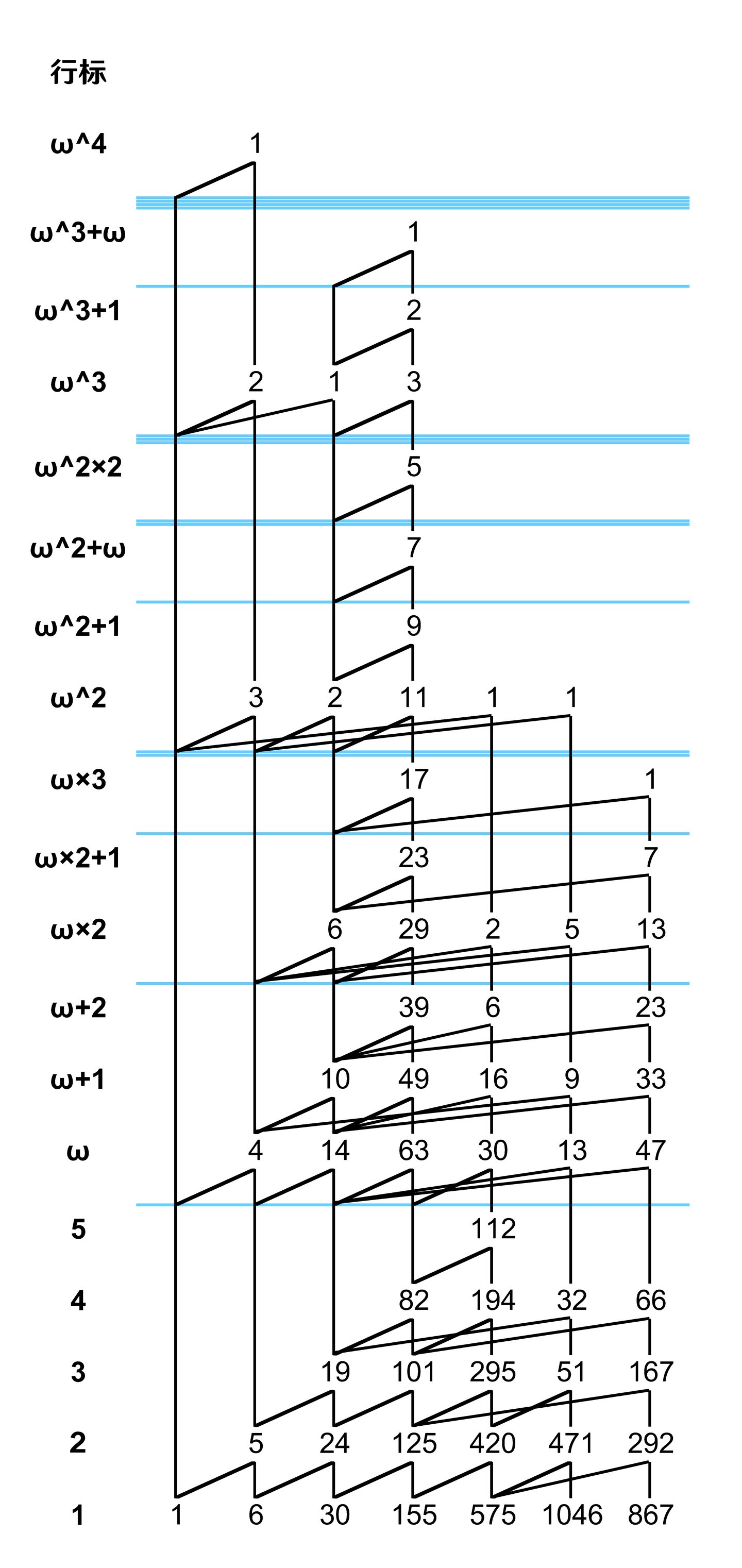
ω-Y 的山脉图中,父项、左腿、右腿、阶差等含义与 0-Y、1-Y 完全一致,这里不做重复介绍。
一般来说,ω-Y 的山脉图具有以下特点:
- 不进行提取操作。提取操作的目的可以说是让“本来找不到父项的项”有机会与其它项位于同一行,从而可以找到父项。而在标准的 ω-Y 表达式之中,所有大于 1 的项都可以按规则找到父项。因此,无需进行提取。
- 每一列最顶端的数都是 1。这个特点可以由上一条推理得到。既然每个大于 1 的项都存在父项,那么它和父项之间就会有阶差,而阶差位于这一项的上方。也就是说,只要一个数不是 1,那么它的上面就还会有别的数字。因此,每一列最上方都是 1。反过来,所有的 1 都一定位于所在列的顶端。这一条特点可以作为一个 ω-Y 山脉图是否完整的验证方式。
- 某一项、它的父项、以及它和父项之间的阶差项的行标关系。假设这一项的行标为β,其父项的行标为α,那么: (1) 时:阶差项的行标为 。也就是说,如果该项和父项位于同一行,那么阶差项在它们上面一行,中间相隔一条 0 级分隔线(nothing)。 (2) 时:阶差项的行标为 。也就是说,如果该项和父项不位于同一行,但之间只有 0 级分隔线,那么阶差项在它们上面 行,中间相隔一条 1 级分隔线。 (3) 时:阶差项的行标为 。也就是说,如果该项和父项之间的分隔线等级最高为 n 的话,那么阶差项在它们上面 行,中间相隔一条 n+1 级分隔线。
接下来是通过山脉图找到父项的方法。为了更好地解释找父项的行为,我们需要引入待定父项这一重要概念。值得一提的是,对于具备一定复杂度的记号,“通过待定父项来确定父项”几乎都成为了必不可少的一步。所以,了解这一概念以及它的相关运作方式,不止对 ω-Y 的理解有帮助。
具体地,对于 ω-Y 山脉图中的某一项(记作 X),我们从 X 出发,沿左腿向左下走一步,然后沿右腿向上一直走到行标至多为 X 的行标的位置(有可能一步都走不了),最后停留的位置就是 X 的待定父项。
在 {X, X的待定父项, X的待定父项的待定父项, ...} 形成的序列中,最先遇到的数值小于 X 的项即为 X 的父项。我们算出 X 与其父项的阶差,根据这两项的位置按照上面的规律确定阶差项的位置,然后画出阶差项的左腿和右腿。不断对每一个新生成的项重复这一过程,直到无法这样做,最终就能得到完整的 ω-Y 山脉图。
MEGAwhY mountain 可以绘制 ω-Y 的山脉图。
展开
概念介绍:
为了更好地介绍 ω-Y 的展开,我们又不得不又引入一些新的概念以及对 1-Y 中的概念做出一些修正:
根元素、根列:山脉图的最右列最上方元素所连接的左腿所指的元素,称为根元素。其所在的列为根列。
根列元素:位于根列的、行标小于等于根元素行标的元素,称为根列元素。
作用区域:假设所有根列元素的行标从小到大依次为 ,那么对于行标为 的元素,其作用区域为根列(含)向右、行标从 (含元素,不含其下方的边)到 (不含元素,含其下方的边)的区域。 被规定为山脉最右列最上方元素所在的行标。每一个根列元素都与一块作用区域一一对应,并且这些作用区域相互不重叠。
轮廓边:从一个根列元素出发,沿左腿向上一步(但不能超出这个根列元素的作用区域)之后,沿右腿向下若干步(可以不向下,但同样不能超出这个根列元素的作用区域),随后重复这个过程直到无路可走。能通过这样的操作经过的边,都是这个根列元素对应的(或者这个作用区域内的)移动边。这些边的特点是,复制时左右腿连接的对象均会移动。
非轮廓边:经过了某个作用区域,但不符合这个作用区域内轮廓边的概念的边,称为这个作用区域内的固定边。这些边的特点是,复制时左腿连接的对象保持不变。
填充边:从一个根列元素出发,沿左腿向上走一行后,沿右腿向下走一行,随后重复这个过程直到无路可走。能通过这样的操作经过的边,称为这个根列元素对应的填充边。填充边属于移动边。
行差:在本文,我们约定第 行和第 行()的行差为满足 的序数 。例如,第 行和第 行的行差为 ,第 行和第 行的行差为 。
一个根列元素,对应了一块作用区域、一组轮廓边和一组填充边。
展开规则:
在展开ω-Y时,我们先将末列减一,然后从上到下依次处理每一个作用区域。对于每一个作用区域,我们依次进行以下操作:
轮廓边的复制:我们将轮廓边的端点及其所指的元素向右上方进行复制。具体地,向右平移(末列位置-根列位置)的列数,然后向上平移至满足以下条件的位置:若平移前端点所指的元素与根列元素行差为,那么平移后对应端点所指的元素与末列最上方的元素行差也要为。像这样,直至所有的轮廓边和它们所指的元素都被复制到了新的位置上。
填充边的复制:如果上一步中中,末列最上方元素与根列元素的行差为0,那么无需复制填充边,直接跳过这一步。否则,需要将轮廓边向上移动所造成的空位使用填充边进行填补。具体的做法与1-Y的填充是类似的,但从上向下进行,并且需要处理填补极限序数行时,左右脚的行差问题。
非轮廓边的复制
这些边的复制最后进行。它们的左腿指向的元素都保持不动,而右腿向右或右上平移。向右平移的列数依旧是(末列位置-根列位置)。如果这条非轮廓边右腿所指元素没有被这个作用区域内的轮廓边所指到,那么无需向上平移;如果有,那么向上平移到与末列最上方元素行差为的位置。这里的依旧是平移之前该元素与根列元素的行差。
重复这三步的操作(注意每次操作时末列的位置和作用区域内末列最上方元素的行标会变化),我们便能得到指定ω-Y表达式的基本列。
运算实例
ω-Y(1,3,10,29,36) 的展开:首先,画出 ω-Y(1,3,10,29,36) 的山脉图,如图 2:
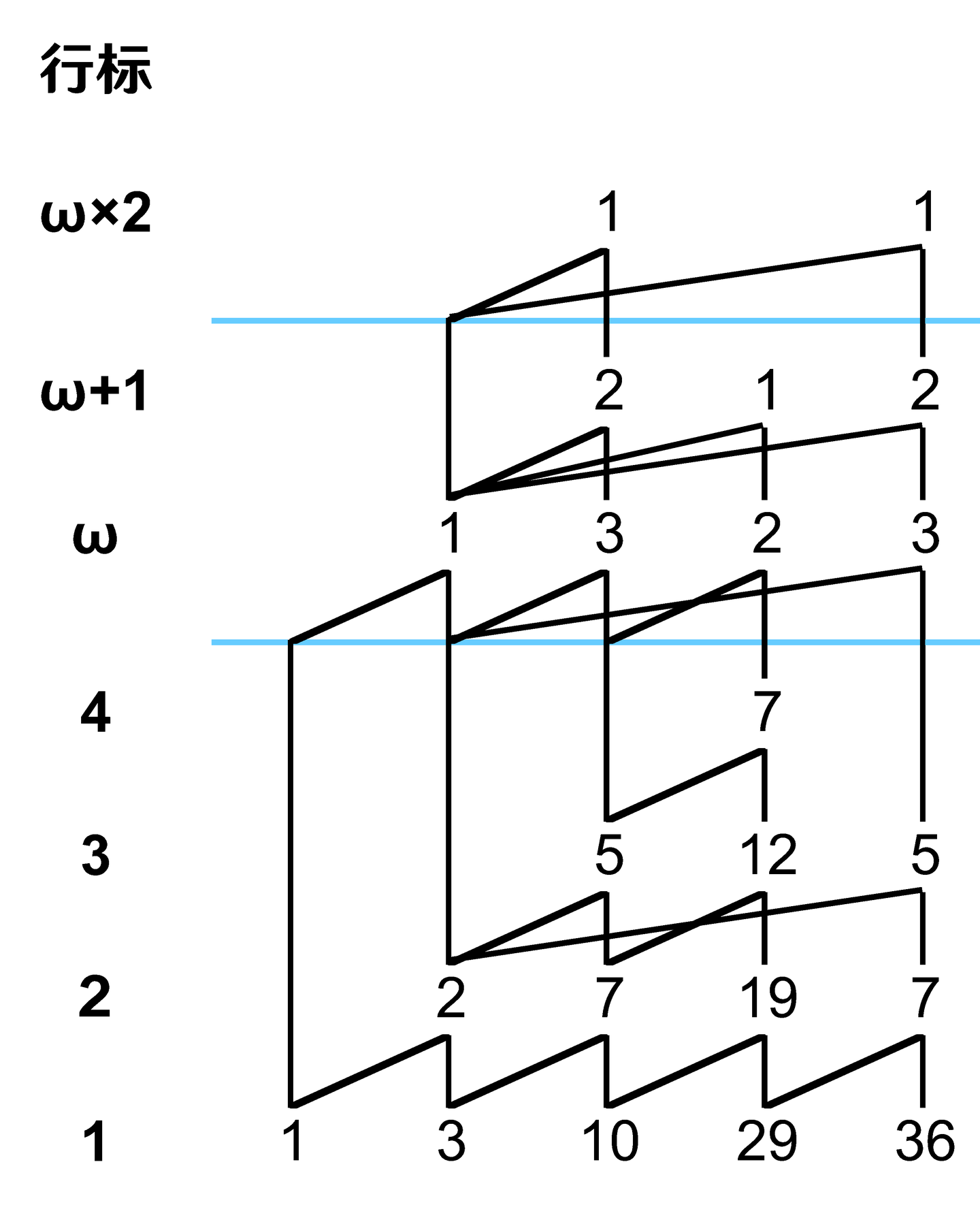
显然,根列是第二列,根元素为第二列第 行的 1。因此,这个山脉图中有三个根列元素,需要划分出三个作用区域,如图 3 所示。
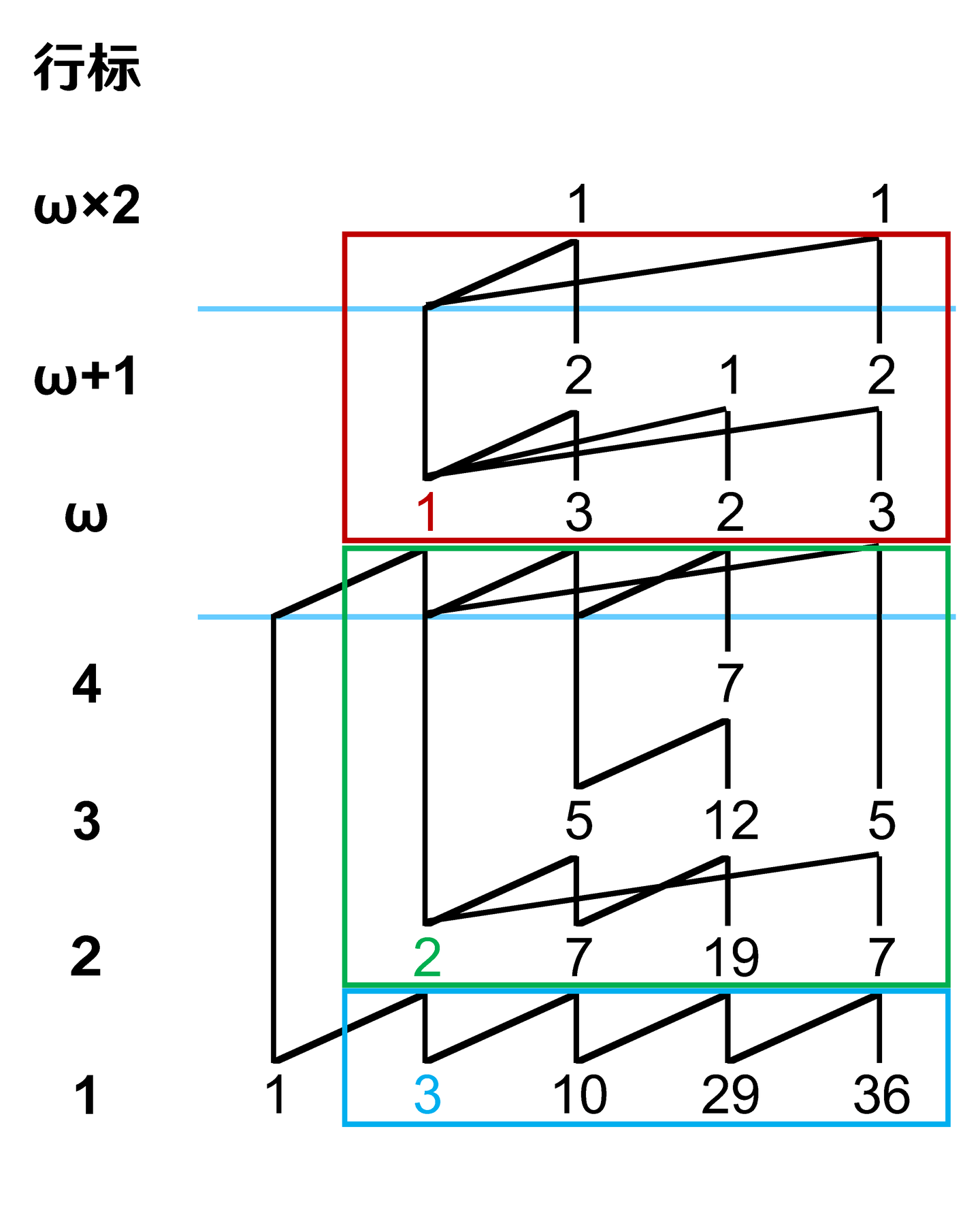
接着,我们就按照前面所说的,将末列减一之后,开始从上到下依次处理每一个区域。
对最上方作用区域的处理,首先是对轮廓边进行复制。这一区域内的所有边都是轮廓边,根列元素行标为 ,末列最上方元素行标为 。为了保持行差关系,我们把原来位于 行的元素随着复制平移到 行,把原来位于 行的元素随着复制平移到 行,如图 4 所示:
这样一个简单的平移就完成了。注意,无论何时,作用区域内的东西都不会因为平移被移动到作用区域外。
紧接着进行填充边的复制和填充。我们找到填充边(图5深蓝色),并把它们向右和向右上填补到上一步生成的空隙中去(图5浅蓝色),就像这样:
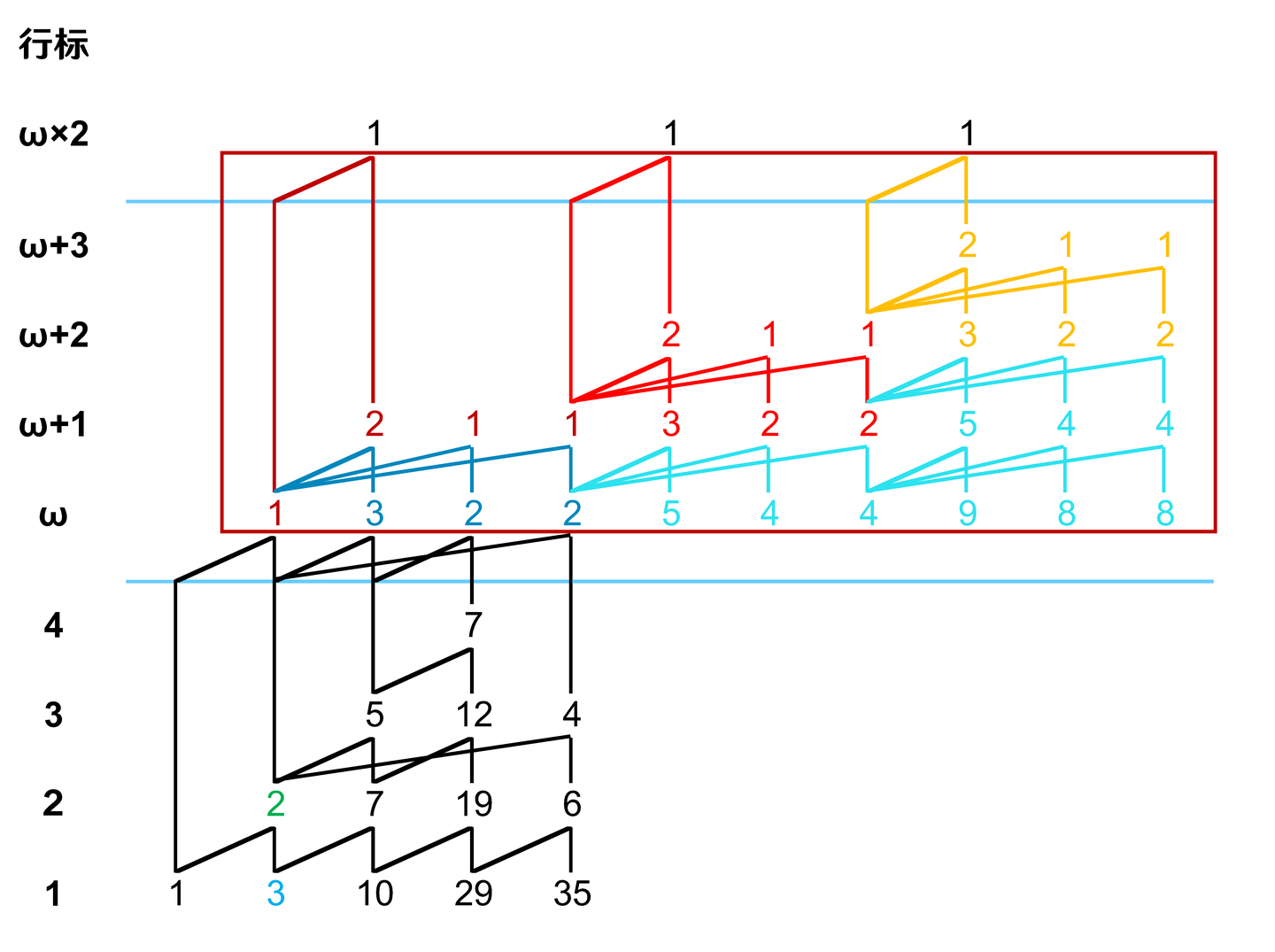
和1-Y中的操作是一样的。毕竟,ω-Y(1,3,10,29,35)还没有超出1-Y极限。
最后是非轮廓边的复制。幸运的是,这一区域不存在非轮廓边,所以我们已经处理完成这一区域了。
对中间的作用区域的处理,还是先对轮廓边进行复制。这一个区域内,仍然所有的边都是轮廓边,根列元素行标为2,末列最上方元素行标为3,因此,我们所需要进行的平移操作和上面是一样的,找到填充边,把空隙填进去,和第一个区域一样。
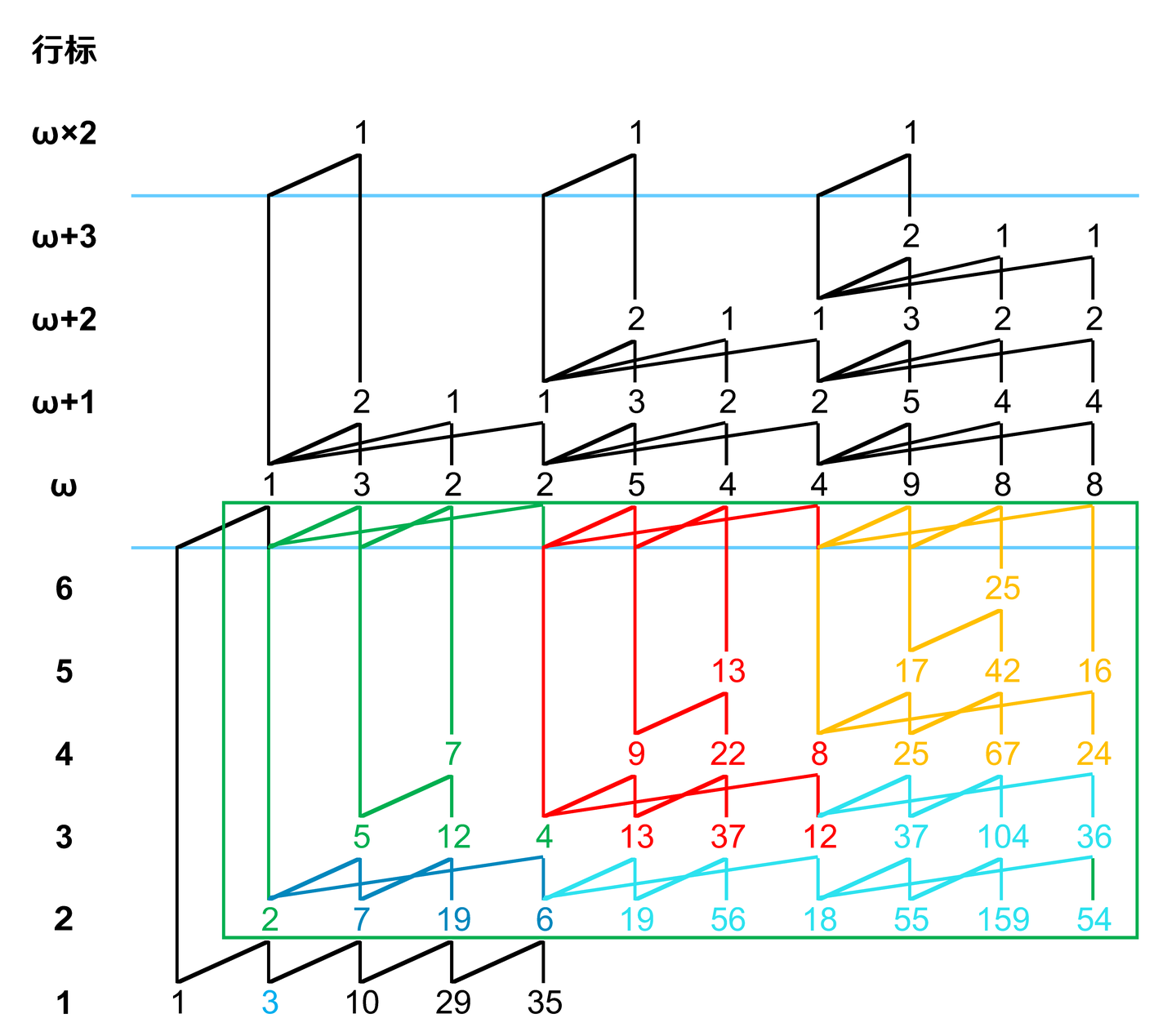
第二个区域依然没有非轮廓边,那么这个区域也结束了。
最下方的区域只有一行,因此不会产生空隙,也就无需搭理填充边。所以,对它的处理也是最简单的。
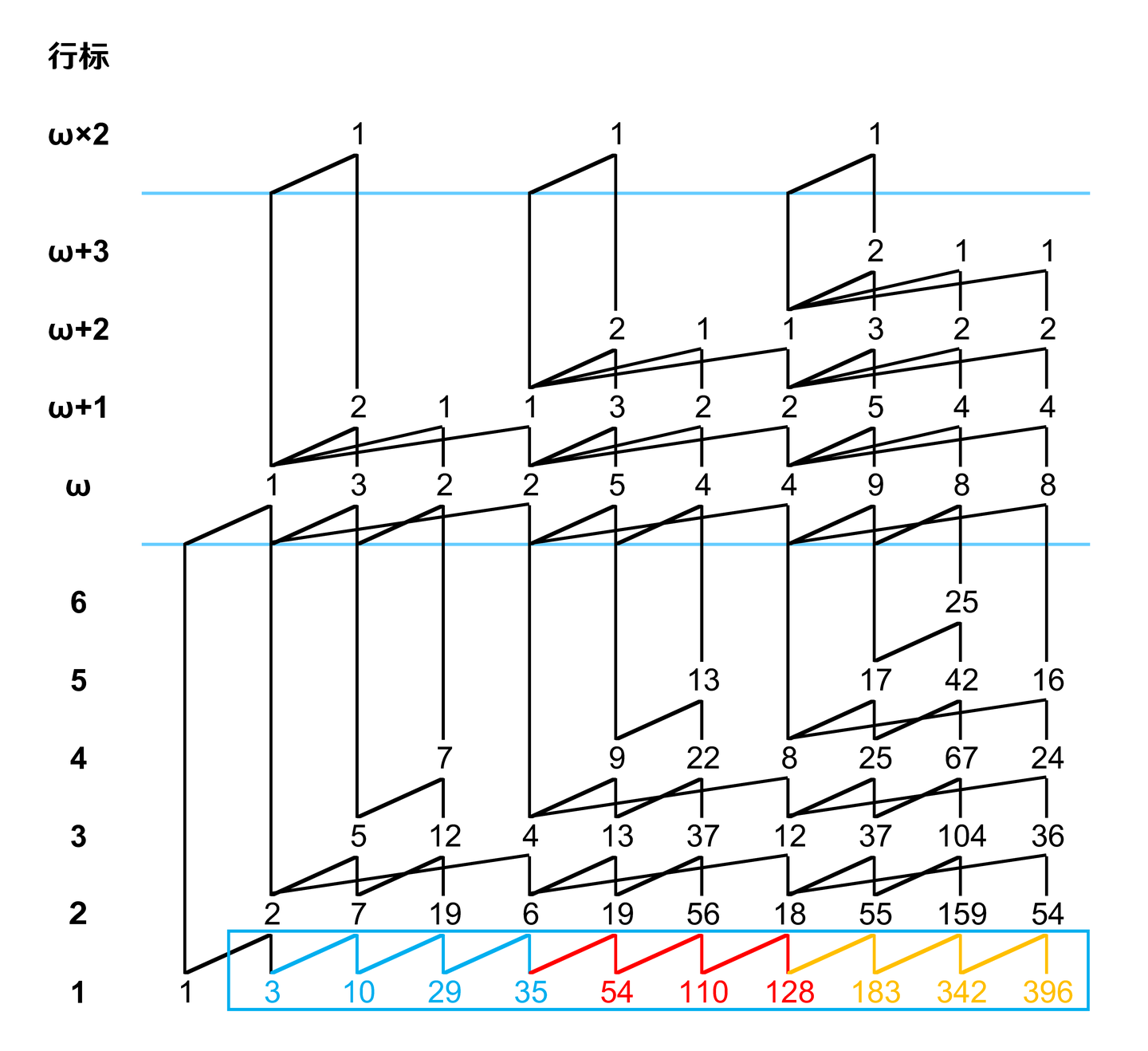
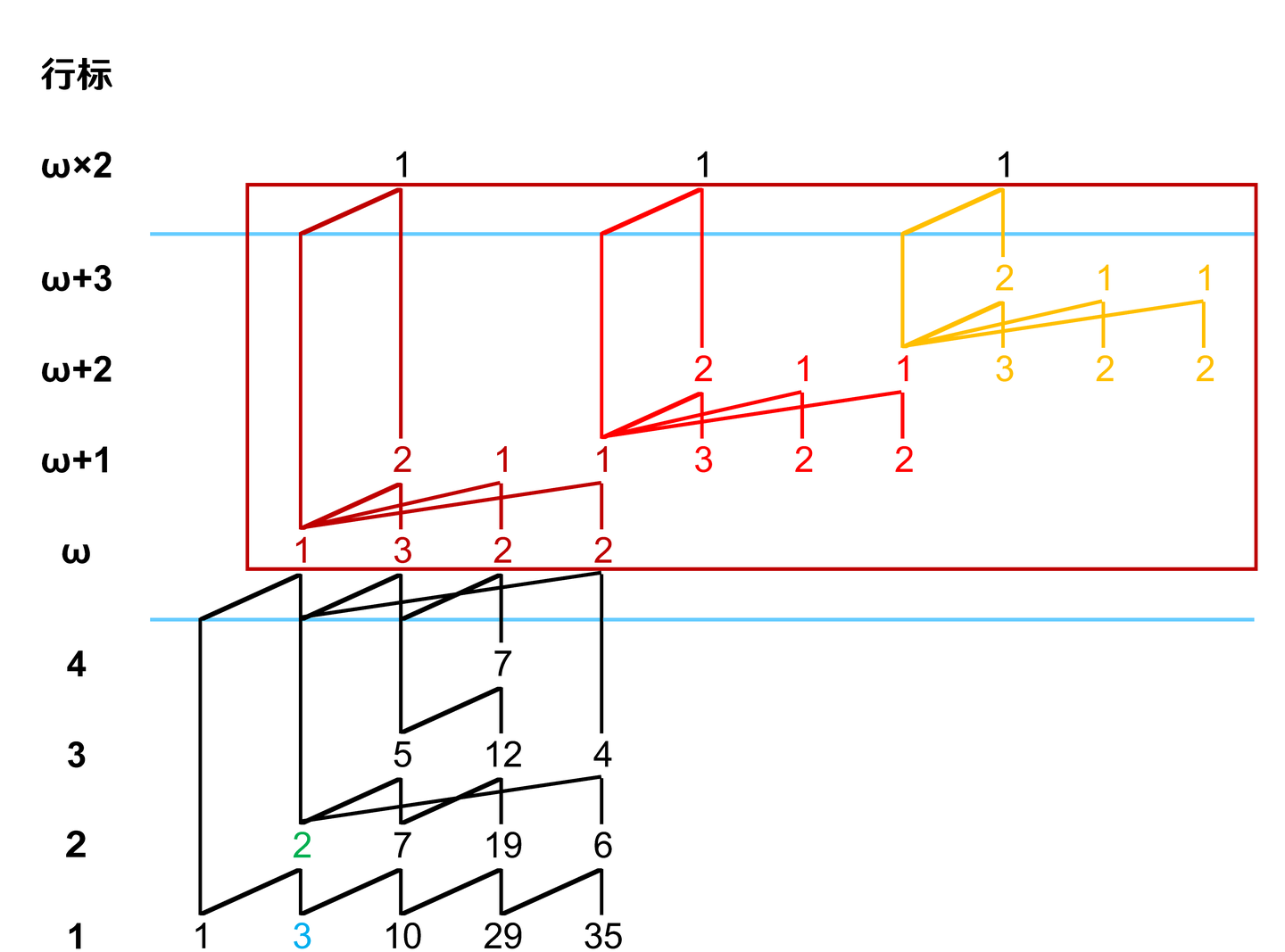
ω-Y(1,4,18,48,32) 的展开:首先,画出山脉图,并标出其中的根列元素、作用区域如下:
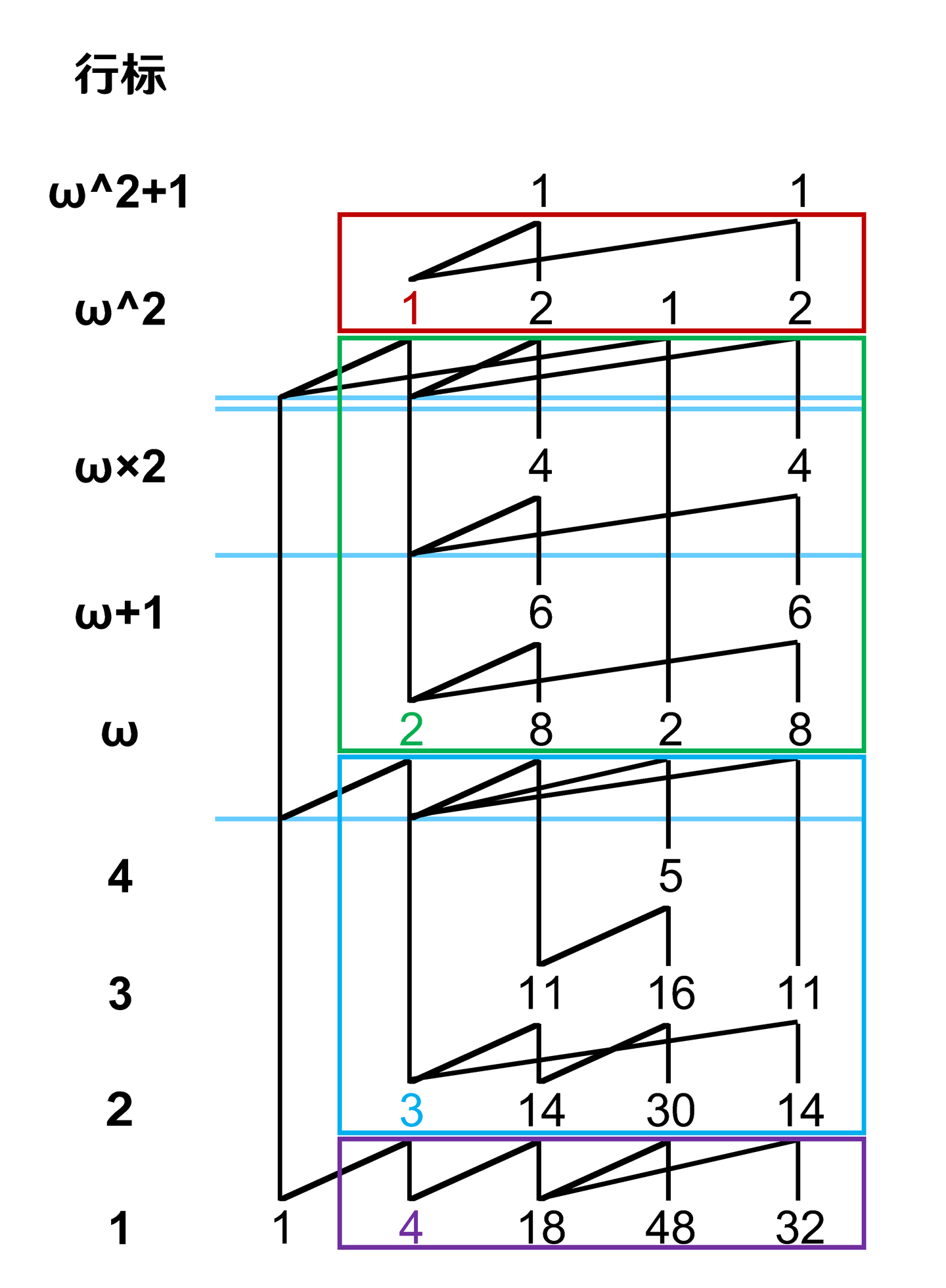
那么,依旧是把最右列减一,然后从上往下处理每一个根列元素。
对最上方作用区域的处理,这个作用区域只有一行。那么是比较简单的,向右平移就好了。
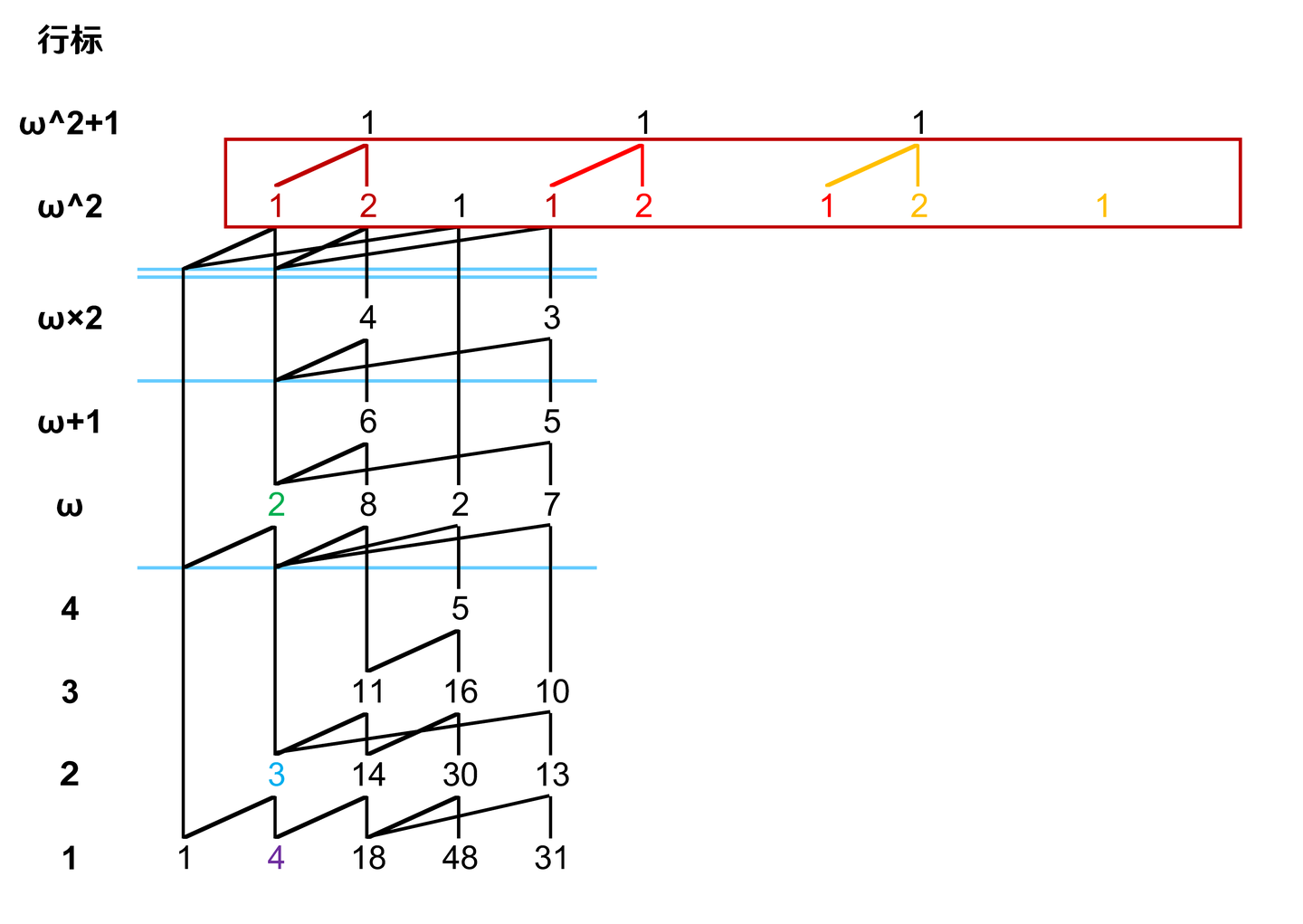
对第二个作用区域的处理,这个作用区域就有些复杂了。不过我们还是按照步骤,先找出所有的轮廓边如下:
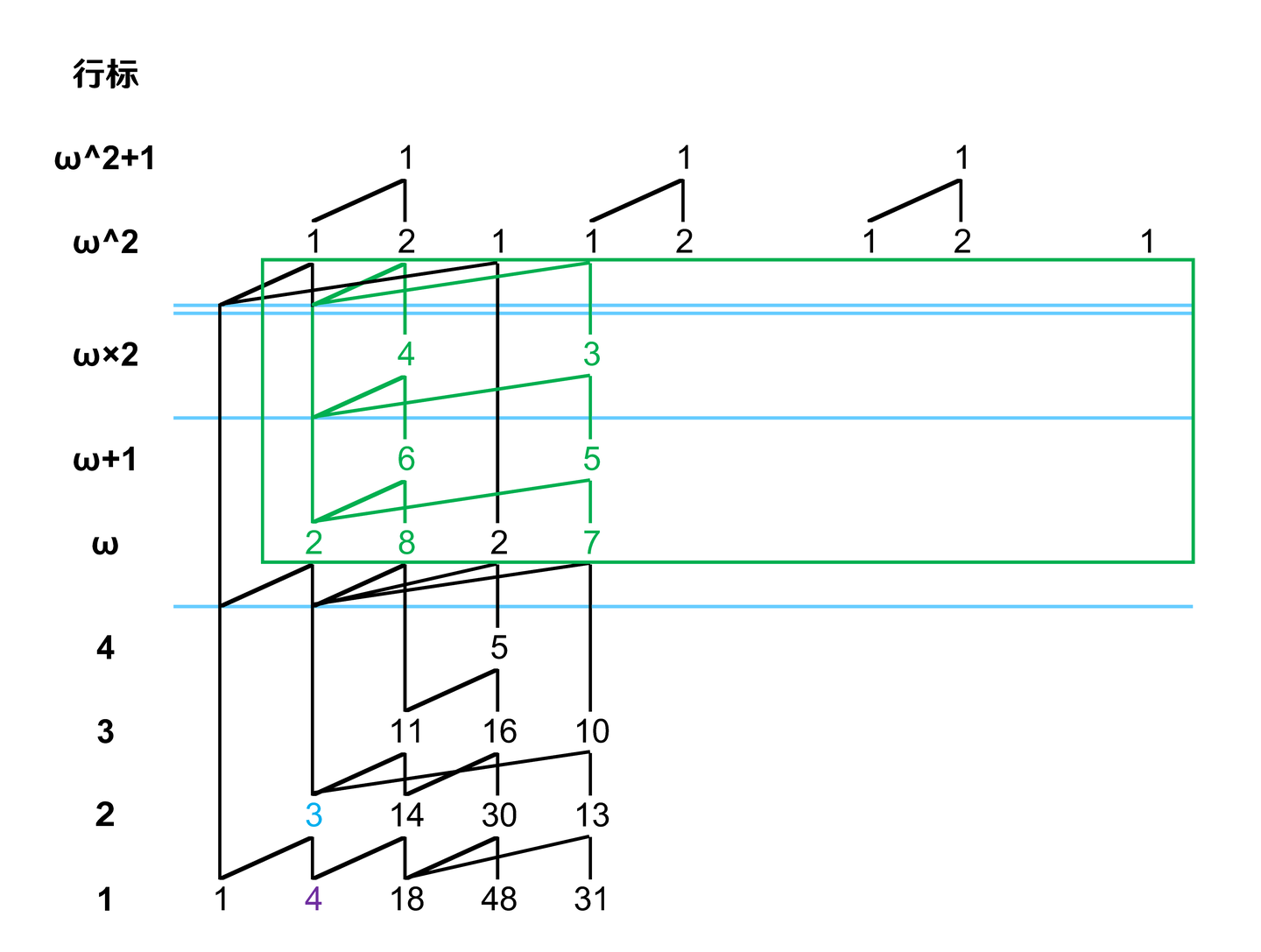
可见,这个作用区域内的根列元素位于第 行,最右列的最上端元素位于第 行。依照相对行差进行平移,我们把原来位于 行的元素随着复制平移到 行,把原来位于 行的元素随着复制平移到 行,把原来位于 行的元素随着复制平移到 行,如图 11 所示。
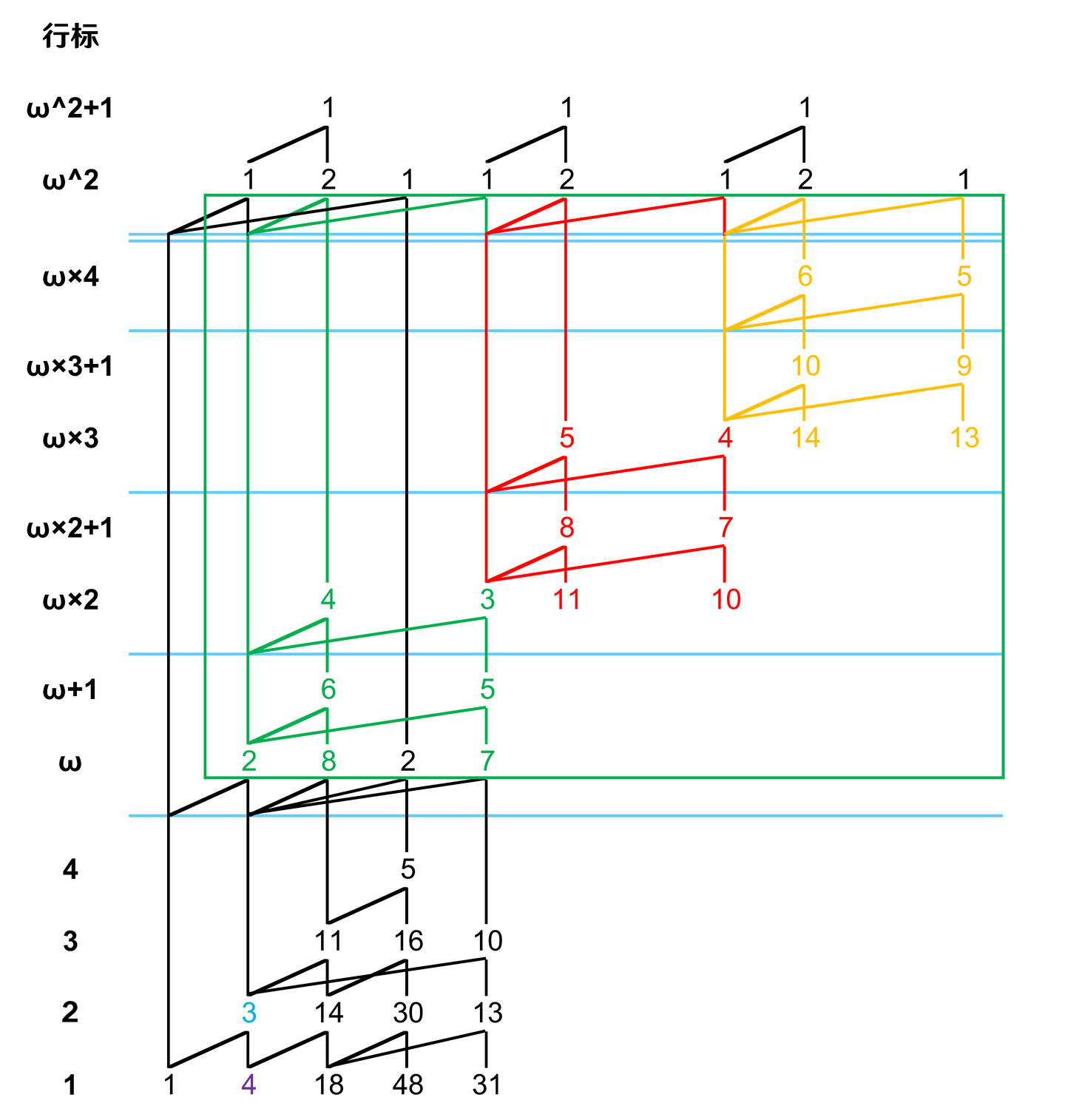
现在,轮廓边复制完成了,轮到填充边。当空隙有多行时,填充边从上往下进行填充。但是,此时出现了一个特殊情况:我们需要把填充边复制到一个跨过了高级(≥1级)分隔线的位置上。为了确保山脉图的行标规则不被破坏,我们规定:当填充边被复制到跨过了 n 级分隔线的位置上时,其左腿和右腿的行差需要为 。按照这个规定,我们先填充红色部分空隙的最上面一行,这样,就多出了一个 行。继续从上往下填充 行和 行的部分,以及按照同样流程完成橙色部分的填充,结束整个填充边复制的步骤。
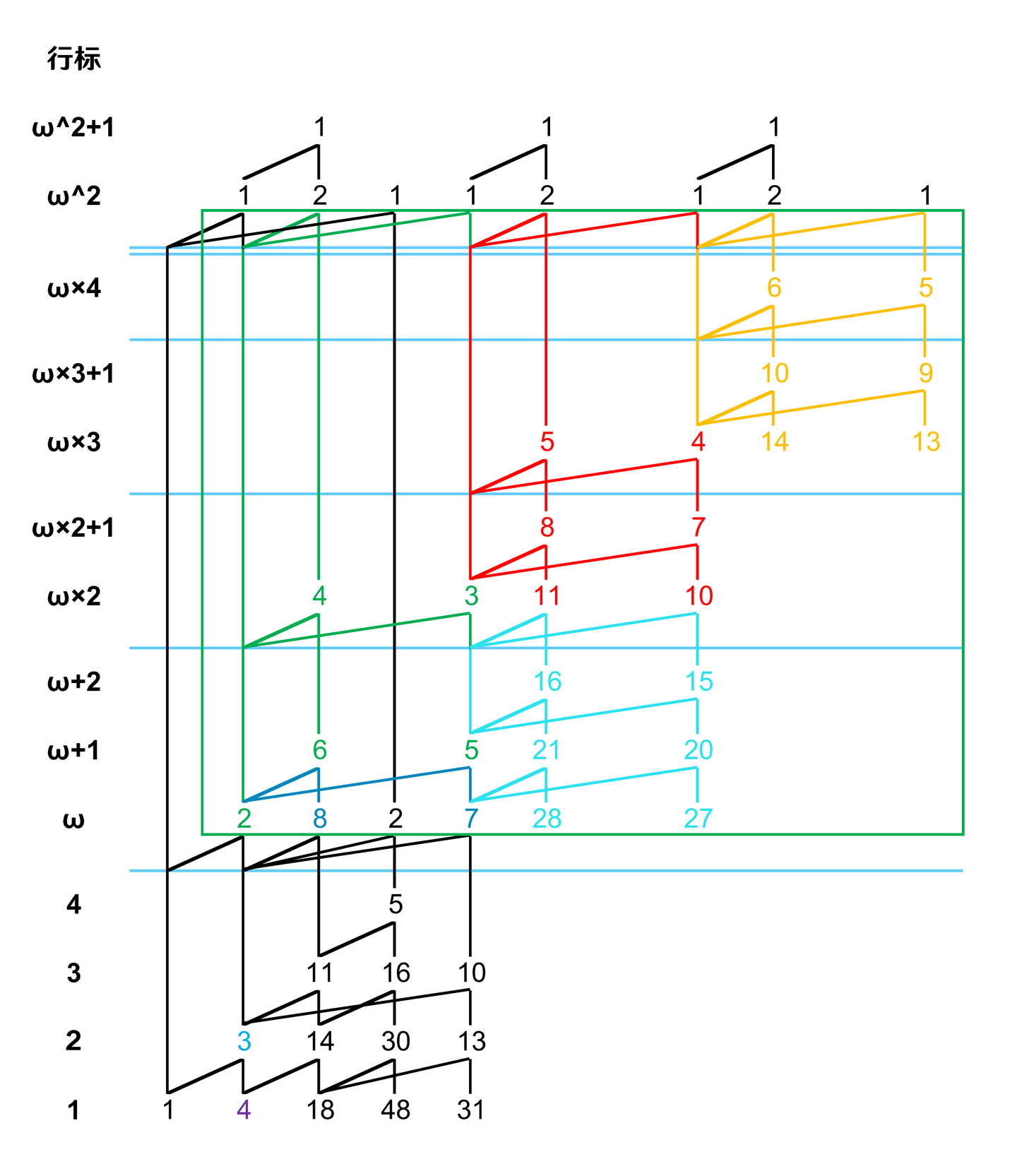
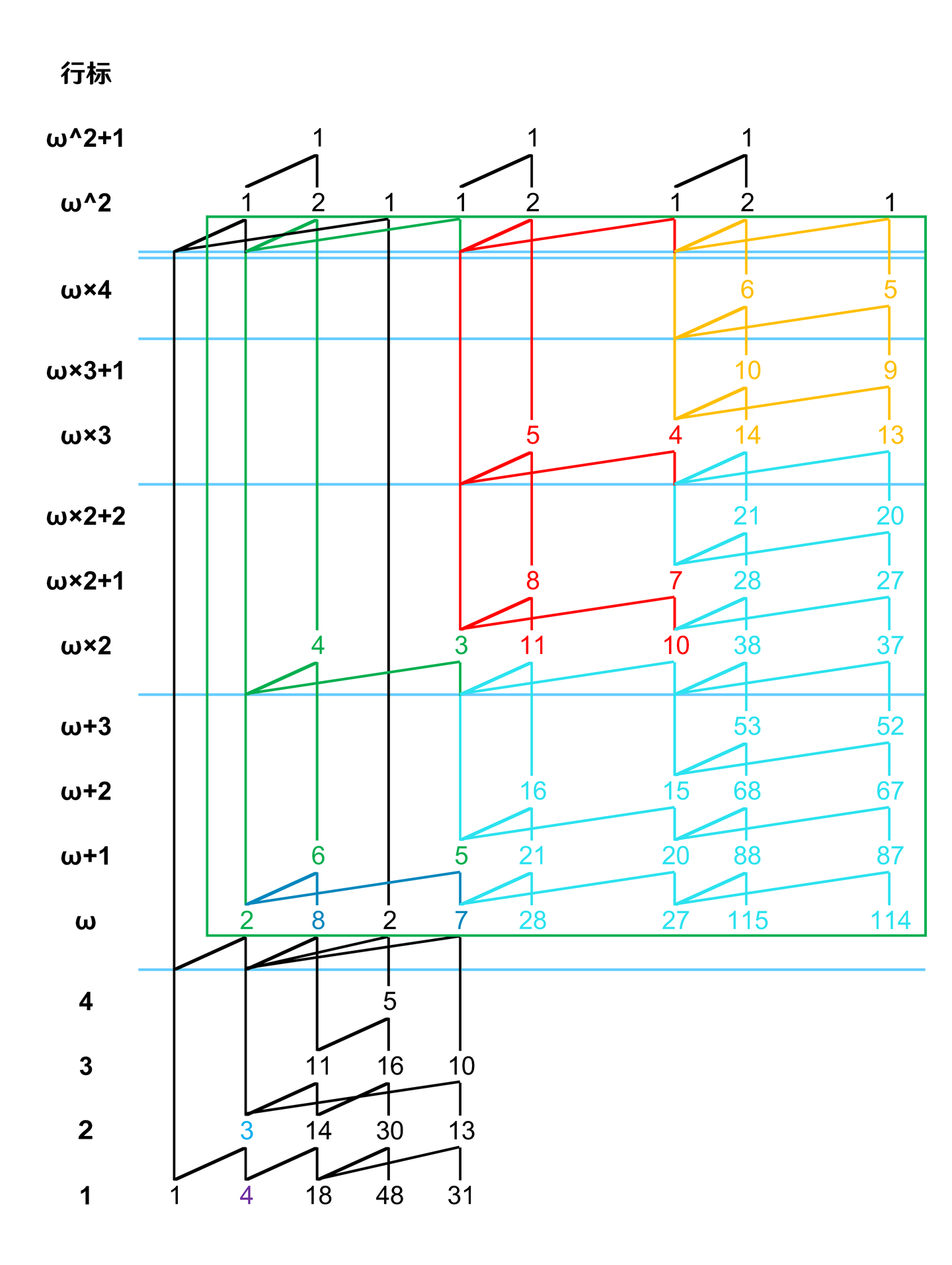
但是第二个区域并没有处理完。在绿色的部分,有一条大黑边与其它的部分格格不入——它是非轮廓边。我们在最后需要对它进行处理。由于它右腿所指的元素并没有被轮廓边指到,所以直接向右平移,就像这样:
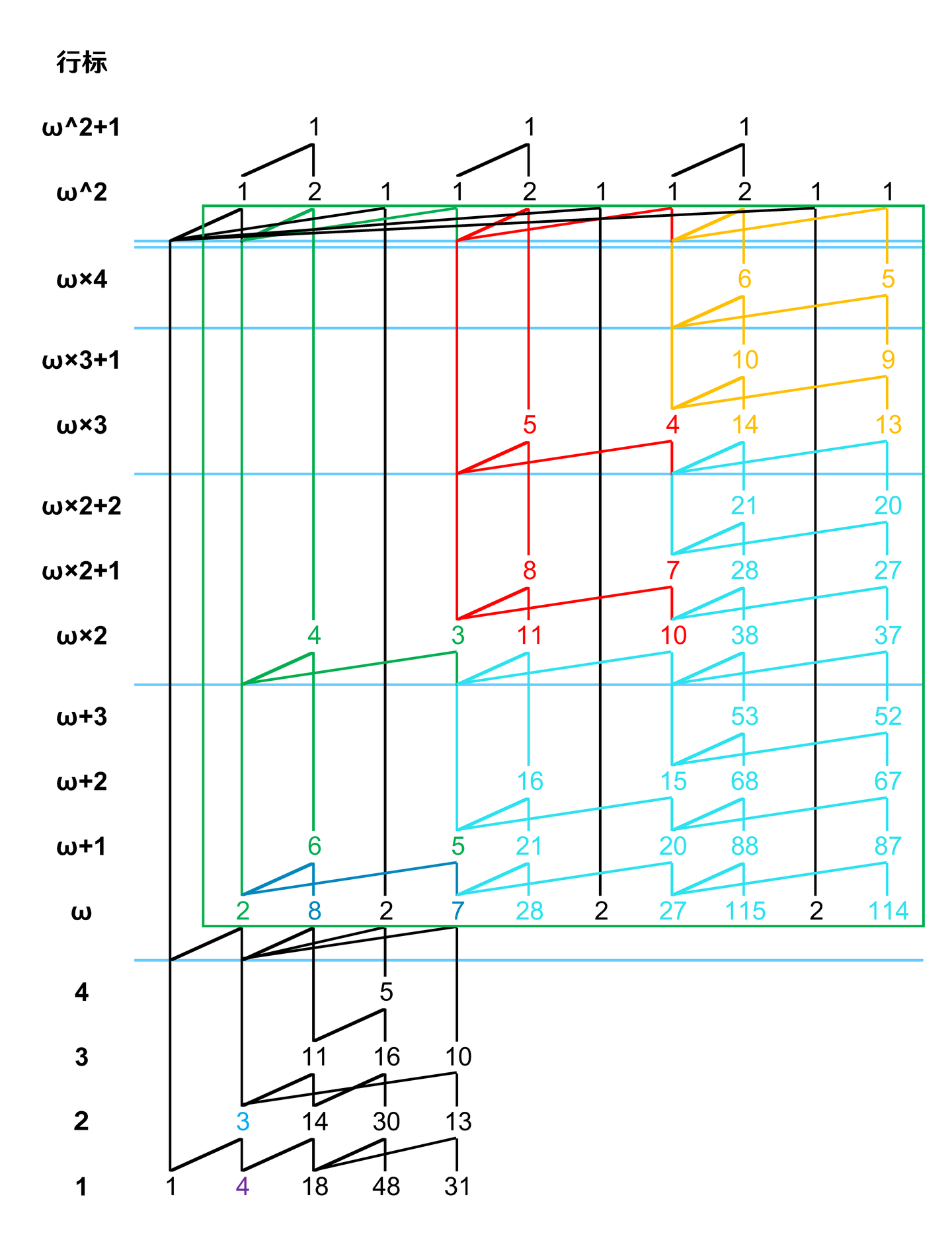
第三和第四个作用区域的复制,这两个区域的边的复制没有什么特殊的行为。
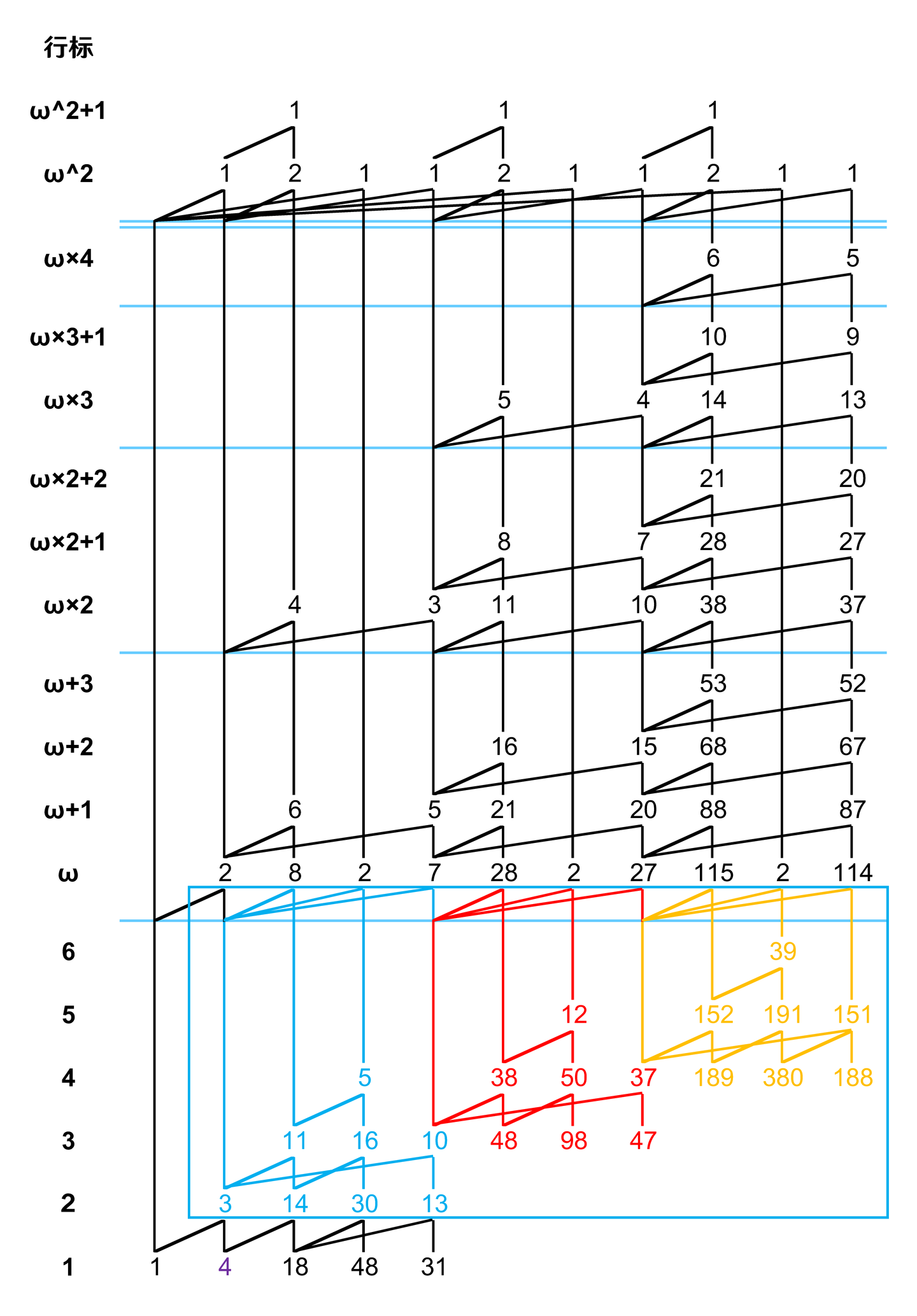
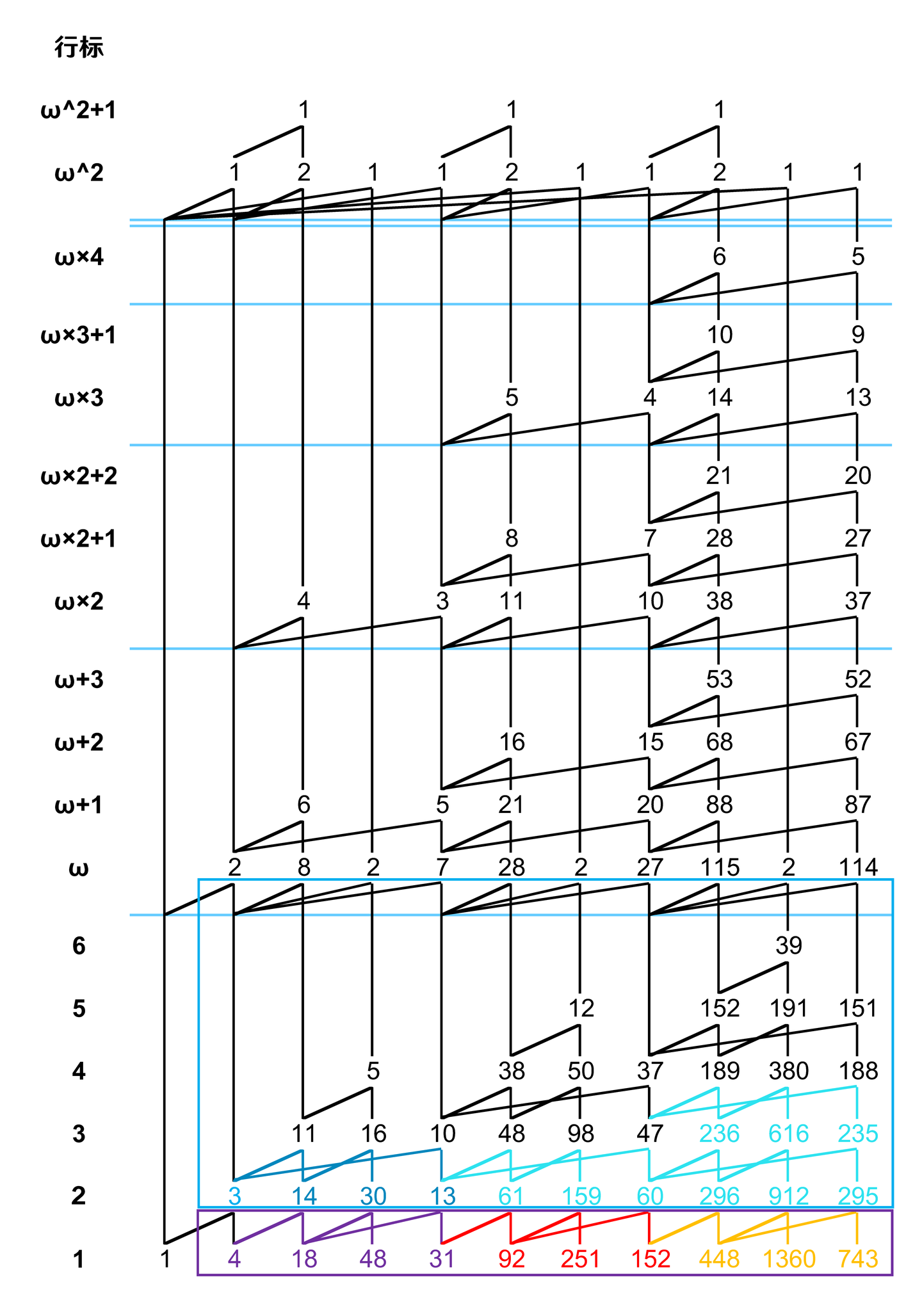
于是我们完成了本例的展开。
n-Y 序列
如果我们在 ω-Y 序列绘制山脉图的过程中绘制完 以下的部分就停止,则这样得到的序列就是 n-Y 序列。n-Y 序列的山脉图只有 行,分隔山脉图的直线最多只有 n 重,它的展开规则与通常的 ω-Y 序列是一致的。n-Y 序列有两个不同的版本,其中 C n-Y (Consistent n−Y) 在绘制山脉图的过程中进行提取操作,而 D n-Y (Diagonlizing n−Y) 在绘制山脉图的过程中不进行提取操作。
对于 C n-Y 来说,我们有
对于 D n-Y 来说,我们有 ,以及 。
Magma
以上介绍的 ω-Y 规则称为 weak magma 规则,它是目前最常用的规则。在未做说明的情况下,我们默认 ω −Y 的规则就是 weak magma 规则。除了 weak magma 规则之外,还有三种与之并列的规则,它们分别为 medium magma 规则,strong magma 规则以及 actual规则。在历史上,actual 规则是最先提出的,其余三种规则是之后提出的。而在现在看来,除了 weak magma 之外的三种规则基本已经被淘汰了,它们已经几乎只有历史上的意义了。
下面我们简要介绍上述四种规则的区别。我们引入 ω-Y 原版定义中的 magma 元素、wildfire 边、eruption 边以及 magma 边的概念(这与上面给出定义的顶点元素、参考边、轮廓边、平移边的概念并不完全相同)。每个根列元素都对应一组 magma 元素和 magma边,有两种不同的方法来对它们进行确定,分别为 weak magma 和 strong magma 两种规则。
- weak magma 的确定规则如下:从一个根列元素出发,沿左腿往右上方走一步(可能有多种走法),然后沿右腿向下走一步,如果到达了与根列元素同一行的复制部分,这个元素就是 magma 元素。从 magma 元素出发也(递归地)走同样的路。所有经过的边就是 magma 边。
- strong magma 的确定规则如下:从一个根列元素出发,沿右腿向下走一步,然后沿左腿往右上方走一步(可能有多种走法),如果到达了与根列元素同一行的复制部分,这个元素就是 magma 元素。从 magma 元素出发也(递归地)走同样的路。所有经过的边就是 magma 边。
作出新边的过程,可以分成 3 种不同的边,它们分别为 wildfire 边、eruption 边、magma边,这些边都是从复制部分复制出来的。其中,wildfire 边通常高度是不变的;eruption 边高度会提高,但数量仍与复制源相同;而 magma 边则会从一个复制源复制出许多份。而 weak magma 和 strong magma 两种规则在 magma 边的复制规则处又有所不同。
- weak magma 的复制规则如下:对每个 magma 元素,先沿右腿向上走一步,然后沿左腿向下一步,这个左腿就是我们接下来要复制的复制源。
- strong magma 的复制规则如下:对每个 magma 元素,直接沿左腿向下一步。这个左腿就是我们接下来要复制的复制源。
至此我们就可以区分出四种不同 ω-Y 的规则如下。
- weak magma ω − Y 的规则为:展开用的是 weak magma 规则,最初确定 magma 元素的时候用的也是 weak magma 规则。
- strong magma ω − Y 的规则为:展开用的是 strong magma 规则,最初确定 magma元素的时候用的也是 strong magma 规则。
- medium magma ω − Y 的规则为:展开用的是 strong magma 规则,最初确定 magma元素的时候用的是 weak magma 规则。
- actual ω − Y 的规则为:展开用的是 strong magma 规则;最初确定 magma 元素的时候,如果根列元素位于后继序数行(包括第 1 行)就用 strong magma 规则,否则用weak magma 规则。
这四种规则的 ω-Y 可以用 Notation Explorer 展开。目前已知 weak、strong、medium 三种 magma 的 ω-Y 在 1,3,8 即 catch。
主词条:ω-Y magma 对比分析