传递

“传递”，全称序数结构传递现象，是一个在序数记号中出现的现象，与序数本身没有联系。“传递”一般描述一个序数记号表达式在展开时，不仅仅是判定展开所用到的元素参与了展开过程，还有别的元素也参与了展开过程。

解释

一个关于“传递”的典型例子是BOCF。我们发现 $ψ (1) \times (n + 1) = ψ (1) \times n + ψ (0) + ψ (0) + ψ (0) + \dots$ ，是对一个基础的序数增加一系列 $ψ (0)$ ，那么 $ψ (2)$ 的展开是否也是对一个基础的序数增加一系列 $ψ (0)$ 呢？如果是的话， $ψ (2) = ψ (1) + ψ (0) + ψ (0) + ψ (0) + \dots$ ，这明显和BOCF的定义不符。如果只有【形如 $ψ (α + 1)$ 的B hydra表达式可以确定展开式】这一条规则，我们只需要判断ψ里面的东西是不是有一个+1就知道展开式是什么了，而不需要管那个 $α$ 是多少；但是在 $ψ (2) = ψ (1) + ψ (1) + ψ (1) + ψ (1) + \dots$ 里面，展开规则不仅管了ψ里面的东西是不是有一个+1，还涉及到了那个 $α + 1$ 的 $α$ 是多少，这就是“传递”。

不过也有人更倾向于用PrSS解释传递： $1, 2, . . ., 1, 2$ ，不管省略号里面是什么东西，这个表达式的展开都是把末尾的2变为 $1, 1, 1, 1, 1, . . .$ ；那么在 $1, 2, 2$ 中，应该也遵循这样的规则，即 $1, 2, 2 = 1, 2, 1, 1, 1, 1, 1, . . .$ 。其实不然，1,2,2展开为什么，不仅取决于坏根，还取决于坏根之后的一些元素，这才让 $1, 2, 2 = 1, 2, 1, 2, 1, 2, 1, 2, . . .$ 成为可能。

传递和迭代的关系

在4年前或者更久之前，array notation主导整个googology。在那个时候，构造大自然数有3条基本规则：基础运算、迭代、对角化。线性SAN中， $s (a, b) = a^{b}$ ，这是基础运算； $s (a, b + 1, c + 1, #) = s (a, s (a, b, c + 1, #), c, #)$ ，这是迭代； $s (a, b, 1, 1, 1, . . ., 1, c + 1, #) = s (a, b, b, b, b, . . ., b, c, #)$ ，这是对角化。

考虑线性SAN里对应迭代的规则： $s (a, b + 1, c + 1) = s (a, s (a, b, c + 1, #), c)$ ，这是三项的SAN，在一步展开后，第二项变成了一个新的三项SAN表达式。到了四项SAN， $s (a, b + 1, c + 1, d)$ ，在一步展开后，第二项应该也是变成了一个新的三项SAN表达式吧？显然不是， $s (a, b + 1, c + 1, d) = s (a, s (a, b, c + 1, d), c, d)$ ，第二项变成了四项的SAN表达式。但是我们只需要前三项就可以用迭代规则展开了，为什么第四项还要在迭代时放进展开式里呢？

这个问题，和在前面传递里讲到的“PrSS的1,2,2只需要坏根1和末项2就可以展开，为什么还要带上中间那个2呢？”，很明显是同一个东西！所以，构造大自然数有3条基本规则，基础运算、迭代、对角化，来到构造大递归序数之后，变成了新的3条基本规则：后继、传递、对角化。

“传递”这个词的英文翻译目前还比较混乱，因为传递就是迭代这件事，在2024年12月初才被发现。刚刚发现传递的时候（2024年2月），直接机翻为transmitting，例如FOSnt中的t就是它的缩写；到了3月，传递的英文逐渐被remaining替代，这个名字由ProjectCF提出，虽然不那么符合除基本列序数序列之外的记号，但还是沿用到了12月，使用在了“著名”但早已不再使用的RD序列系统中的R。在发现传递就是迭代后，318'4开始将传递直接译作iterating。

传递按行数分类

PrSS的 $1, 2, 2 = 1, 2, 1, 2, 1, 2, . . .$ 和BOCF的 $ψ (2) = ψ (1) \times n$ 只是最表层的传递，后面还有更多种类的传递。

因为差分序列有明确的“行”的概念，所以这里以差分序列（和BMS）为例。表层传递，指的就是PrSS中存在的这种传递，或者叫1行传递，因为它在1行的BMS中就可以见到。

到了LPrSS，传递就没有那么容易发现了。LPrSS的 $1, 3, 5 = 1, 3, 4, 5, 6, 7, 8, 9, . . .$ ，有何不妥吗？只要看向每一项减去它的父项的值，组成阶差序列，就可以看出端倪： $1, 3, 5$ 阶差是 $1, 2, 2$ ，但 $1, 3, 4, 5, 6, 7, 8, 9, . . .$ 却是 $1, 2, 1, 1, 1, 1, 1, 1, . . .$ ，这就是失去传递了。对于0-Y， $1, 3, 5 = 1, 3, 4, 6, 7, 9, 10, 12, . . .$ 阶差序列恰好是 $1, 2, 2 = 1, 2, 1, 2, 1, 2, 1, 2, . . .$ ，是没有失去这种传递的例子。这样的传递，叫做2行传递，因为至少2行BMS才能见到它。

实际上，BMS里最小的2行传递就是 $ζ_{0} = (0) (1, 1) (2, 1)$ ，这就让 $(0) (1, 1) (2, 1) (3)$ 可以突然从 $ζ_{0}$ 增加到 $φ (ω, 0)$ 。同理，BMS里也有3行传递，最小的例子是 $(0) (1, 1, 1) (2, 2, 1)$ ，它略微上方的 $(0) (1, 1, 1) (2, 2, 1) (3)$ ,即SDO，是一个巨大的记号坟墓，这正是3行传递强度的体现。BMS有任意n行的传递，都是首次出现在 $(0) (1, 1, . . ., 1, 1) (2, 2, . . ., 2, 1)$ 。

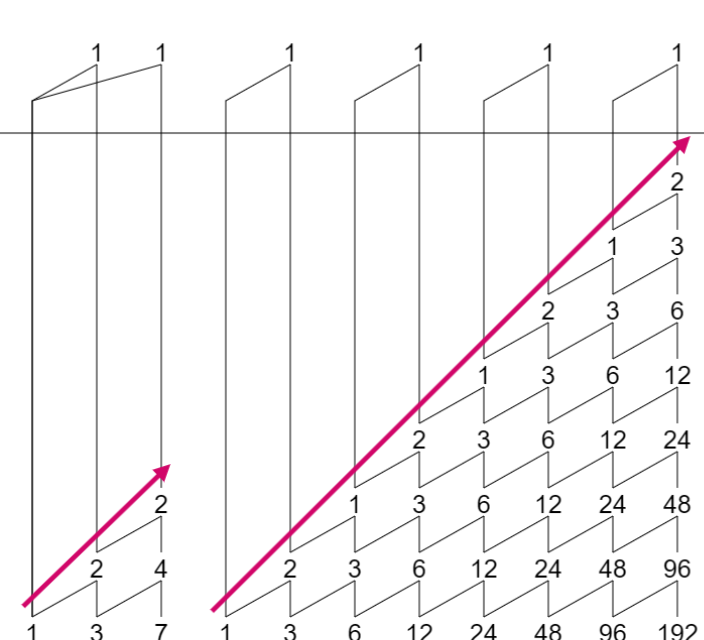
接下来跨越BMS，来到Y序列。我们暂时不考虑 $1, 3, 4, 3$ 提升，包括它下面的 $1, 3, 4, 2, 5, 7, 5$ 提升也先不考虑。这样下来， $1, 3, 7$ 对应 $ω^{2}$ 行BMS，那么序数行BMS能达到Y的高度吗？差太远了，即便失去 $1, 3, 4, 3$ 和 $1, 3, 4, 2, 5, 7, 5$ 提升， $α \to α 行 B M S$ 也只有 $1, 3, 7, 8, 11, 18, 20$ ，刚刚超过 $1, 3, 7$ 一点点，为什么呢？

看向 $Y (1, 3, 7)$ 的展开式，注意那个斜着的 $1, 2, 2 = 1, 2, 1, 2, 1, 2, 1, 2, . . .$ ，你会发现，这确实是一种传递，但似乎比任意的n行传递都要更强，那这是什么传递呢？跨行传递，或者叫 $ω$ 行传递。

我们严谨的定义BMS与ω-Y中的传递如下，值得注意的是，基于weak magma ω-Y的α to β传递的定义依然有部分争议：

基于BMS的a to b传递的定义：对于一个BMS表达式，末列最下方非0元素所在行记作b，删掉某行以及所有大于它的行之后，导致坏根发生变化，或在存在和不存在之间切换。有这样效果的行中的最大者记作a，如果表达式有这样的行a，那么就说这个表达式是一个a to b结构传递，否则说这个表达式没有结构传递。

基于weak magma ω-Y的α to β传递的定义：先重新规定ω-Y山脉图的第一行(也就是原序列)行标为0而不是1。然后LNZ沿用通用的定义，坏根定义为LNZ的左腿所在列，如果LNZ的左腿不存在，那坏根也不存在。对于一个ω-Y表达式(标准或不标准)的完整山脉图，LNZ所在行记作β，删掉某行以及所有大于它的行之后，导致坏根发生变化，或在存在和不存在之间切换，有这样效果的行中的最大者记作α。如果表达式有这样的行α，那么就说这个表达式是一个α to β结构传递，否则说这个表达式没有结构传递。

接下来到了Y序列也没有的传递：ω^ω行传递。在Notation Explorer中，看Defective ω·2 mountain notation；已知 $() (; 1) = () (, 1) (, 2,, 2) (, 3,, 3,,, 3) (, 4,, 4,,, 4,,,, 4) . . .$ 等于ω-Y，那么 $() (; 1) (, 2; 1) = () (; 1) (, 2) (, 3; 3) (, 4,, 4) (, 5,, 5; 5) . . .$ 还能用ω-Y描述吗？显然，这个传递在Y的视角下，就和 $Y (1, 3, 7)$ 这个传递在BMS视角下一样，这是更弱的记号完全无法理解的传递。

在按行数分类的传递里面，一般序数越整，传递越强，例如强度：ω^ω行传递>ω²行传递>ω行传递>2行传递。