0-Y

$\mathrm{0}\mathrm{-}\mathrm{Y}$是一种 Worm 型序数记号，它是 PrSS 与 BMS 的一种扩展。

定义

合法表达式

一个合法的 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 表达式是以 1 开头的正整数序列，即形如

$(a_1,a_2,\cdots ,a_n)(n,a_1,a_2,\cdots ,a_n\in \mathbb{\mathbb{N}},a_1=1)$

的序列。

例如：$(1,4,6,4)$和 $(1,1,4,5,1,4)$ 都是合法的 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 表达式，而 $(1,2,\pi )$ 不是。

结构

$\mathrm{0}\mathrm{-}\mathrm{Y}$ 的合法表达式可分为零表达式、后继表达式和极限表达式。

• 零表达式指 $n=0$ 的表达式，即空序列；
• 后继表达式指 $n>0,a_n=1$ 的表达式，即末项为 1 的非空序列；
• 极限表达式指 $n>0,a_n>1$ 的表达式，末项不为 1 的非空序列。

对于 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 的一个极限表达式 $(a_1,a_2,\cdots ,a_n)$，定义以下术语：

行标与列标

设想我们在一个无限大的矩阵下工作，从左往右是第 1,2,... 列，从下往上是第 0,1,... 行。第 $i$ 行第 $j$ 列的项记为 $x_{i,j}$。

初始时，我们有 $x_{0,j}=a_j$，$1\le j\le n$。

父项与阶差项

等于 1 的项没有父项。对于大于 1 的项$x_{i,j}$，它的父项与它位于同一行，且是满足以下条件的最右侧项 $x_{i,k}$：

• $k<j$ 且 $x_{i,k}<x_{i,j}$。
• 如果 $i>0$，还要求 $x_{i-1,k}$ 是 $x_{i-1,j}$ 的祖先项。

这里“祖先项”的定义类似于 BMS：一个元素自己，以及它的父项、父项的父项、父项的父项的父项......共同构成它的祖先项。

对于 $x_{i,j}$，如果它有父项 $x_{i,k}$，则它的阶差项为 $x_{i+1,j}=x_{i,j}-x_{i,k}$；如果 $x_{i,j}=1$，则它的阶差项 $x_{i+1,j}=1$。

由于第 $i$ 行的项的阶差项构成了第 $i+1$ 行，称第 $i+1$ 行的序列是第 $i$ 行的序列的阶差序列。

末列与坏根

第 $n$ 列称为末列。

对于末列的某一项 $x_{i,n}$，它的父项设为 $x_{i,r}$。如果在计算到某行（第 $p$ 行）时有 $x_{p,n}-x_{p,r}=1$，则称 $a_r$ 为坏根，称第 $r$ 列为根列，并且不再计算第 $p+1$ 行及之后的行。

以上给出了 $\mathrm{0}\mathrm{-}\mathrm{Y}$极限表达式 $(a_1,a_2,\cdots ,a_n)$ 的完整寻找坏根流程。

山脉图

要描述 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 的展开规则，需要用到山脉图的辅助。对于 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 的一个极限表达式 $(a_1,a_2,\cdots ,a_n)$，它的山脉图的画法如下：

先按照寻找坏根的规则画出第 0 到 $p$ 行。现在你有了一个 $p\times n$ 的“矩阵”（第 0 至第 $p$ 行，第 1 至第 $n$ 列），接下来，对于第 $i$ 行，$0\le i\le p-1$ 进行如下操作：

对于每个 $x_{i,j}$，用竖直线段连接 $x_{i+1,j}$ 的下端与 $x_{i,j}$ 的上端。这些竖直线段称为右腿，$x_{i,j}$ 称为它的端点。

对于每个大于 1 的 $x_{i,j}$，设 $x_{i,j}$ 有父项 $x_{i,k}$，用斜线段连接 $x_{i+1,j}$ 的下端与 $x_{i,k}$ 的上端。这些斜线段称为左腿，$x_{i,k}$ 称为它的端点。

对第 1 到第 $p$ 行各执行一次上述操作，就得到了 $(a_1,a_2,\cdots ,a_n)$ 的山脉图。

山脉图有以下性质：从一个有父项的元素出发，沿右腿向上走一步，再沿左腿向下走一步，就能到达它的父项。

注意：有些情况下，山脉图只包含一行，即第 0 行。

注：由于山脉图的某一行只和其下的项有关，你也可以在逐行往上填写阶差序列的同时画出山脉图。许多常见的 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 教程都采用这个方法。

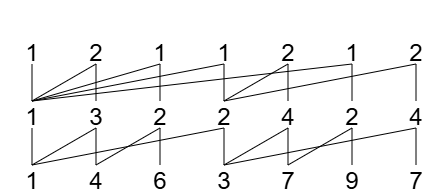
以 $\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,3,7,9,7)$ 为例，其山脉图如右图所示。由于第2行末项2的阶差为1，故不再继续计算。

展开

对于 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 的一个表达式 $(a_1,a_2,\cdots ,a_n)$：

• 如果它是零表达式，它对应序数 0。
• 如果它是后继表达式，它对应 $(a_1,a_2,\cdots ,a_{n-1})$ 的后继。
• 如果它是极限表达式，它的基本列第 $q$ 项如下确定：
  1. 作出 $p\times n$ 的山脉图。称位于根列右侧的结构（包括阶差项和其对应的山脉图中的左右腿，不包括根列）为坏部，其余为好部。
  2. 删除坏部中第 $p$ 行以下的所有项，并将 $x_{p,n}$ 减 1。
  3. 接下来，保留山脉图的好部不动，将坏部平移并复制在山脉图末尾，复制 $q-1$ 次。“坏部平移”是指左右腿及端点同时平移。
  4. 特别地，如果某一条左腿的端点位于根列左侧，复制时左腿的端点不向右平移。
  5. 接下来，你得到了根列右侧的一系列山脉图和第 $p$ 行的一系列项。从根列右侧开始，从上到下，每一行从左到右，按照以下方式填入正整数：对于某个位置，向上通过右腿移动到值为 $x$ 的项，然后向左下通过左腿移动到值为 $y$ 的项，则回到初始位置并填上 $x+y$。
  6. 最后得到的第 0 行的序列，就是 $(a_1,a_2,\cdots ,a_n)$ 展开的基本列第 $q-1$ 项。

$\mathrm{0}\mathrm{-}\mathrm{Y}$ 的极限基本列是 $\{(1,2),(1,3),(1,4),\cdots \}$，从这个基本列中元素开始取前驱或取基本列所能得到的表达式是 0-Y 的标准式。

例 1：$\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,4)[3]$

先作出它的山脉图，从图中可以得到：根列为第 1 列，坏部为第 2、3、4 列。

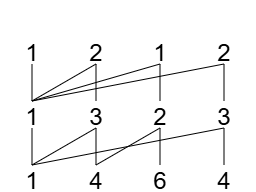
然后，将坏部第 2 行以下的数删除，并将其整体平移并复制 2 次。

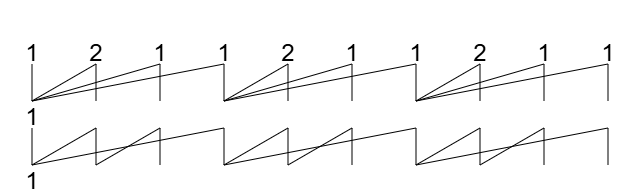
接着，依次向山脉图中的“空位”填入正整数，注意所填的数满足“一个数等于其右腿和左腿连接的数之差”。

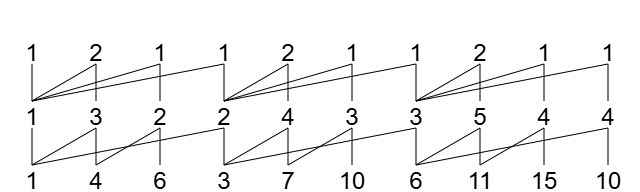
最后，根据山脉图的第 0 行，我们得到了 $\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,4)[3]=\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,3,7,10,6,11,15,10)$。

例 2：$\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,3,7,9,7)[3]$

其山脉图已经在前面给出。从图中可以得到：根列为第 4 列，坏部为第 5、6、7 列。

注意：第 2 行第 6 列的“1”的左腿的另一端（位于第 1 列）在根列左侧，故在复制时，其另一端点保持不动。

复制、填充后得到的山脉图如下。

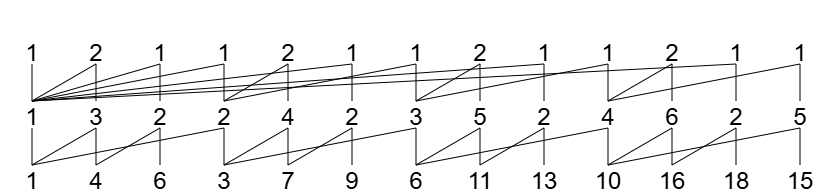
因此 $\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,3,7,9,7)[3]=\mathrm{0}\mathrm{-}\mathrm{Y}(1,4,6,3,7,9,6,11,13,10,16,18,15)$

枚举

我们使用 BMS 对 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 进行简单分析（左边是 $\mathrm{B}\mathrm{M}\mathrm{S}$，右边是 $\mathrm{0}\mathrm{-}\mathrm{Y}$）。

$(0)=1$

$(0)(1)=1,2$

$(0)(1)(1)=1,2,2$

$(0)(1)(2)=1,2,3$

$(0)(1)(2)(3)=1,2,3,4$

$(0)(1,1)=1,3$

$(0)(1,1)(1,0)=1,3,2$

$(0)(1,1)(1,0)(2,1)=1,3,2,4$

$(0)(1,1)(1,1)=1,3,3$

$(0)(1,1)(2,0)=1,3,4$

$(0)(1,1)(2,0)(3,1)=1,3,4,6$

$(0)(1,1)(2,1)=1,3,5$

$(0)(1,1)(2,1)(3,1)=1,3,5,7$

$(0)(1,1)(2,2)=1,3,6$

$(0)(1,1)(2,2)(3,3)=1,3,6,10$

$(0)(1,1,1)=1,4$

$(0)(1,1,1)(1,0,0)(2,1,1)=1,4,2,5$

$(0)(1,1,1)(1,1,0)=1,4,3$

$(0)(1,1,1)(1,1,0)(2,2,1)=1,4,3,7$

$(0)(1,1,1)(1,1,1)=1,4,4$

$(0)(1,1,1)(2,0,0)=1,4,5$

$(0)(1,1,1)(2,1,0)=1,4,6$

$(0)(1,1,1)(2,1,0)(1,1,1)=1,4,6,4$

$(0)(1,1,1)(2,1,0)(3,1,0)=1,4,6,8$

$(0)(1,1,1)(2,1,0)(3,2,1)=1,4,6,10$

$(0)(1,1,1)(2,1,1)=1,4,7$

$(0)(1,1,1)(2,1,1)(3,1,1)=1,4,7,10$

$(0)(1,1,1)(2,2,0)=1,4,8$

$(0)(1,1,1)(2,2,1)=1,4,9$

$(0)(1,1,1)(2,2,2)=1,4,10$

$(0)(1,1,1)(2,2,2)(3,3,3)=1,4,10,20$

$(0)(1,1,1,1)=1,5$

$(0)(1,1,1,1,1)=1,6$

$\cdots$

两者极限相等。

与 BMS 的互译

事实上，$\mathrm{0}\mathrm{-}\mathrm{Y}$ 与 BMS 的标准式之间有十分简单的互译关系。

对于一个 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 标准表达式，作出其山脉图，但不考虑末列的影响，而是无限地逐行向上作出阶差序列，直到得到的序列全为 1。

现在你有了一个 $t\times n$ 的山脉图，行标为 0 到 $t$，列标为 1 到 $n$。

定义 $b_{i,j}$ 如下：

• $x_{i,j}=1$ 时 $b_{i,j}=0$
• 否则设 $x_{i,j}$ 的父项为 $x_{i,k}$，令 $b_{i,j}=b_{i,k}+1$

最后得到的矩阵 $(b_{i,j})$ 删去最顶上全为 0 的行，并以水平线为轴镜像，即可得到等价的 $\mathrm{B}\mathrm{M}\mathrm{S}$。

对于一个 $\mathrm{B}\mathrm{M}\mathrm{S}$ 标准式 $(d_{i,j})$（第 1 至第 $t$ 行，第 1 至第 $n$ 列），定义 $e_{i,j}$ 如下：

• $d_{i,j}=0$ 时 $e_{i,j}=1$
• 否则设 $d_{i,j}$ 的父项为 $d_{i,k}$，令 $e_{i,j}=e_{i,k}+e_{i+1,j}$（如果 $i=t$，我们规定 $e_{i+1,j}=1$）

最后取出 $f_k=e_{1,k}$，即为等价的 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 序列。

然而，尽管目前已有的分析均支持以上结论，目前对此尚未有严格的证明。

$\mathrm{B}\mathrm{M}\mathrm{S}$ 和 $\mathrm{0}\mathrm{-}\mathrm{Y}$ 的互相转换可以使用 BMS 0-Y Converter Made By FiveYearGaoKao。

与 Y 序列 的关系

$\mathrm{0}\mathrm{-}\mathrm{Y}$ 虽然名字里带有 Y，但它与 Y 序列的内核有较大差异。

历史上，$\mathrm{0}\mathrm{-}\mathrm{Y}$ 的出现晚于通常的 $\mathrm{Y}$ 序列，而且强度也远低于 $\mathrm{Y}$ 序列。事实上，$\mathrm{0}\mathrm{-}\mathrm{Y}$ 是仿照 $\mathrm{B}\mathrm{M}\mathrm{S}$ 制作出来的。