0-Y:修订间差异
更多操作
Apocalypse(留言 | 贡献) 创建页面,内容为“'''0-Y'''是一种Worm型序数记号,它是PrSS的一种扩展。 == 定义 == === 合法表达式 === 一个合法的 0-Y 表达式是以 1 开头的正整数序列,即形如 <math>(a_1,a_2,\cdots,a_n)\quad(n,a_1,a_2,\cdots,a_n\in\N,a_1=1)</math> 的序列。 例如:<math>(1,4,6,4)</math>和<math>(1,1,4,5,1,4)</math>都是合法的 0-Y 表达式,而<math>(1,2,\pi)</math>不是。 === 结构 === 0-Y…” |
|||
| (未显示6个用户的10个中间版本) | |||
| 第1行: | 第1行: | ||
<math>\mathrm{0-Y}</math>是一种 [[Beklemishev's Worm|Worm]] 型[[序数记号]],它是 [[初等序列系统|PrSS]] 与 [[BMS]] 的一种扩展。 | |||
== 定义 == | == 定义 == | ||
=== 合法表达式 === | === 合法表达式 === | ||
一个合法的 0-Y 表达式是以 1 开头的正整数序列,即形如 | 一个合法的 <math>\mathrm{0-Y}</math> 表达式是以 1 开头的正整数序列,即形如 | ||
<math>(a_1,a_2,\cdots,a_n)\quad(n,a_1,a_2,\cdots,a_n\in\N,a_1=1)</math> | <math>(a_1,a_2,\cdots,a_n)\quad(n,a_1,a_2,\cdots,a_n\in\N,a_1=1)</math> | ||
| 第10行: | 第10行: | ||
的序列。 | 的序列。 | ||
例如:<math>(1,4,6,4)</math>和<math>(1,1,4,5,1,4)</math>都是合法的 0-Y 表达式,而<math>(1,2,\pi)</math>不是。 | 例如:<math>(1,4,6,4)</math>和 <math>(1,1,4,5,1,4)</math> 都是合法的 <math>\mathrm{0-Y}</math> 表达式,而 <math>(1,2,\pi)</math> 不是。 | ||
=== 结构 === | === 结构 === | ||
0- | <math>\mathrm{0-Y}</math> 的合法表达式可分为'''零表达式'''、'''后继表达式'''和'''极限表达式'''。 | ||
* '''零表达式'''指<math>n=0</math>的表达式,即空序列; | * '''零表达式'''指 <math>n=0</math> 的表达式,即空序列; | ||
* '''后继表达式'''指<math>n>0,a_n=1</math> | * '''后继表达式'''指 <math>n>0,a_n=1</math> 的表达式,即末项为 1 的非空序列; | ||
* '''极限表达式'''指<math>n>0,a_n>1</math> | * '''极限表达式'''指 <math>n>0,a_n>1</math> 的表达式,末项不为 1 的非空序列。 | ||
对于 0-Y 的一个极限表达式<math>(a_1,a_2,\cdots,a_n)</math>,定义以下术语: | 对于 <math>\mathrm{0-Y}</math> 的一个极限表达式 <math>(a_1,a_2,\cdots,a_n)</math>,定义以下术语: | ||
==== 行标与列标 ==== | ==== 行标与列标 ==== | ||
设想我们在一个无限大的矩阵下工作,从左往右是第 1,2,... 列,从下往上是第 0,1,... 行。第 <math>i</math> 行第 <math>j</math> 列的项记为 <math>x_{i,j}</math>。 | |||
初始时,我们有<math>x_{0,j}=a_j</math>,<math>1\leq{j}\leq{n}</math>。 | 初始时,我们有 <math>x_{0,j}=a_j</math>,<math>1\leq{j}\leq{n}</math>。 | ||
==== 父项与阶差项 ==== | ==== 父项与阶差项 ==== | ||
等于 1 的项没有父项。对于大于 1 的项<math>x_{i,j}</math>,它的父项与它位于同一行,且是满足以下条件的最右侧项 <math>x_{i,k}</math>: | |||
* <math>k<j</math>且<math>x_{i,k}<x_{i,j}</math>。 | * <math>k<j</math> 且 <math>x_{i,k}<x_{i,j}</math>。 | ||
* 如果<math>i>0</math>,还要求<math>x_{i-1,k}</math>是<math>x_{i-1,j}</math>的祖先项。 | * 如果 <math>i>0</math>,还要求 <math>x_{i-1,k}</math> 是 <math>x_{i-1,j}</math> 的祖先项。 | ||
这里“祖先项”的定义类似于[[ | 这里“祖先项”的定义类似于 [[BMS]]:一个元素自己,以及它的父项、父项的父项、父项的父项的父项......共同构成它的祖先项。 | ||
对于<math>x_{i,j}</math>,如果它有父项<math>x_{i,k}</math>,则它的阶差项为<math>x_{i+1,j}=x_{i,j}-x_{i,k}</math>;如果<math>x_{i,j}=1</math>,则它的阶差项<math>x_{i+1,j}=1</math>。 | 对于 <math>x_{i,j}</math>,如果它有父项 <math>x_{i,k}</math>,则它的阶差项为 <math>x_{i+1,j}=x_{i,j}-x_{i,k}</math>;如果 <math>x_{i,j}=1</math>,则它的阶差项 <math>x_{i+1,j}=1</math>。 | ||
由于第<math>i</math>行的项的阶差项构成了第<math>i+1</math>行,称第<math>i+1</math>行的序列是第<math>i</math>行的序列的'''阶差序列'''。 | 由于第 <math>i</math> 行的项的阶差项构成了第 <math>i+1</math> 行,称第 <math>i+1</math> 行的序列是第 <math>i</math> 行的序列的'''阶差序列'''。 | ||
==== 末列与坏根 ==== | ==== 末列与坏根 ==== | ||
第<math>n</math>列称为'''末列'''。 | 第 <math>n</math> 列称为'''末列'''。 | ||
对于末列的某一项<math>x_{i,n}</math>,它的父项设为<math>x_{i,r}</math> | 对于末列的某一项 <math>x_{i,n}</math>,它的父项设为 <math>x_{i,r}</math>。如果在计算到某行(第 <math>p</math> 行)时有 <math>x_{p,n}-x_{p,r}=1</math>,则称 <math>a_r</math> 为'''坏根''',称第 <math>r</math> 列为'''根列''',并且不再计算第 <math>p+1</math> 行及之后的行。 | ||
以上给出了 0-Y 极限表达式<math>(a_1,a_2,\cdots,a_n)</math>的完整寻找坏根流程。 | 以上给出了 <math>\mathrm{0-Y}</math>极限表达式 <math>(a_1,a_2,\cdots,a_n)</math> 的完整寻找坏根流程。 | ||
== 山脉图 == | == 山脉图 == | ||
要描述 <math>\mathrm{0-Y}</math> 的展开规则,需要用到'''山脉图'''的辅助。对于 <math>\mathrm{0-Y}</math> 的一个极限表达式 <math>(a_1,a_2,\cdots,a_n)</math>,它的山脉图的画法如下: | |||
先按照寻找坏根的规则画出第 0 到 <math>p</math> 行。现在你有了一个 <math>p\times{n}</math> 的“矩阵”(第 0 至第 <math>p</math> 行,第 1 至第 <math>n</math> 列),接下来,对于第 <math>i</math> 行,<math>0\leq{i}\leq{p-1}</math> 进行如下操作: | |||
对于每个<math>x_{i,j}</math>,用竖直线段连接<math>x_{i+1,j}</math>的下端与<math>x_{i,j}</math>的上端。这些竖直线段称为'''右腿''',<math>x_{i,j}</math>称为它的端点。 | 对于每个 <math>x_{i,j}</math>,用竖直线段连接 <math>x_{i+1,j}</math> 的下端与 <math>x_{i,j}</math> 的上端。这些竖直线段称为'''右腿''',<math>x_{i,j}</math> 称为它的端点。 | ||
对于每个大于 1 的 <math>x_{i,j}</math>,设 <math>x_{i,j}</math> 有父项 <math>x_{i,k}</math>,用斜线段连接 <math>x_{i+1,j}</math> 的下端与 <math>x_{i,k}</math> 的上端。这些斜线段称为'''左腿''',<math>x_{i,k}</math> 称为它的端点。 | |||
对第 1 到第 <math>p</math> 行各执行一次上述操作,就得到了 <math>(a_1,a_2,\cdots,a_n)</math> 的山脉图。 | |||
山脉图有以下性质:从一个有父项的元素出发,沿右腿向上走一步,再沿左腿向下走一步,就能到达它的父项。 | |||
注意:有些情况下,山脉图只包含一行,即第 0 行。 | |||
注:由于山脉图的某一行只和其下的项有关,你也可以在逐行往上填写阶差序列的同时画出山脉图。许多常见的 <math>\mathrm{0-Y}</math> 教程都采用这个方法。 | |||
[[文件:0y1463797.png|缩略图]] | |||
以 <math>\mathrm{0-Y}(1,4,6,3,7,9,7)</math> 为例,其山脉图如右图所示。由于第2行末项2的阶差为1,故不再继续计算。 | |||
== 展开 == | == 展开 == | ||
对于 0-Y 的一个表达式<math>(a_1,a_2,\cdots,a_n)</math>: | 对于 <math>\mathrm{0-Y}</math> 的一个表达式 <math>(a_1,a_2,\cdots,a_n)</math>: | ||
* 如果它是零表达式,它对应序数 0。 | |||
* 如果它是后继表达式,它对应 <math>(a_1,a_2,\cdots,a_{n-1})</math> 的后继。 | |||
* 如果它是极限表达式,它的基本列第 <math>q</math> 项如下确定: | |||
*# 作出 <math>p\times{n}</math> 的山脉图。称位于根列右侧的结构(包括阶差项和其对应的山脉图中的左右腿,不包括根列)为'''坏部''',其余为'''好部'''。 | |||
*# 删除坏部中第 <math>p</math> 行以下的所有项,并将 <math>x_{p,n}</math> 减 1。 | |||
*# 接下来,保留山脉图的好部不动,将坏部平移并复制在山脉图末尾,复制 <math>q-1</math> 次。“坏部平移”是指左右腿及端点同时平移。 | |||
*# 特别地,如果某一条左腿的端点位于根列左侧,复制时左腿的端点不向右平移。 | |||
*# 接下来,你得到了根列右侧的一系列山脉图和第 <math>p</math> 行的一系列项。从根列右侧开始,从上到下,每一行从左到右,按照以下方式填入正整数:对于某个位置,向上通过右腿移动到值为 <math>x</math> 的项,然后向左下通过左腿移动到值为 <math>y</math> 的项,则回到初始位置并填上 <math>x+y</math>。 | |||
*# 最后得到的第 0 行的序列,就是 <math>(a_1,a_2,\cdots,a_n)</math> 展开的基本列第 <math>q-1</math> 项。 | |||
<math>\mathrm{0-Y}</math> 的极限基本列是 <math>\{(1,2),(1,3),(1,4),\cdots\}</math>,从这个基本列中元素开始取前驱或取基本列所能得到的表达式是 0-Y 的标准式。 | |||
例 1:<math>\mathrm{0-Y}(1,4,6,4)[3]</math> | |||
先作出它的山脉图,从图中可以得到:根列为第 1 列,坏部为第 2、3、4 列。 | |||
[[文件:0-Y(1,4,6,4).png|center|]] | |||
然后,将坏部第 2 行以下的数删除,并将其整体平移并复制 2 次。 | |||
[[文件:0-Y(1,4,6,4)展开(1).png|center|]] | |||
接着,依次向山脉图中的“空位”填入正整数,注意所填的数满足“一个数等于其右腿和左腿连接的数之差”。 | |||
[[文件:0-Y(1,4,6,4)展开(2).png|center|]] | |||
最后,根据山脉图的第 0 行,我们得到了 <math>\mathrm{0-Y}(1,4,6,4)[3]=\mathrm{0-Y}(1,4,6,3,7,10,6,11,15,10)</math>。 | |||
例 2:<math>\mathrm{0-Y}(1,4,6,3,7,9,7)[3]</math> | |||
其山脉图已经在[[0-Y#山脉图|前面]]给出。从图中可以得到:根列为第 4 列,坏部为第 5、6、7 列。 | |||
# | |||
注意:第 2 行第 6 列的“1”的左腿的另一端(位于第 1 列)在根列左侧,故在复制时,其另一端点保持不动。 | |||
复制、填充后得到的山脉图如下。 | |||
[[文件:0-Y(1,4,6,3,7,9,7)展开.png|center|]] | |||
因此 <math>\mathrm{0-Y}(1,4,6,3,7,9,7)[3]=\mathrm{0-Y}(1,4,6,3,7,9,6,11,13,10,16,18,15)</math> | |||
== 枚举 == | == 枚举 == | ||
我们使用 [[ | 我们使用 [[BMS]] 对 <math>\mathrm{0-Y}</math> 进行简单分析(左边是 <math>\mathrm{BMS}</math>,右边是 <math>\mathrm{0-Y}</math>)。 | ||
<math>(0)=1</math> | <math>(0)=1</math> | ||
| 第151行: | 第172行: | ||
两者极限相等。 | 两者极限相等。 | ||
== 与[[ | == 与 [[BMS]] 的互译 == | ||
事实上,<math>\mathrm{0-Y}</math> 与 [[BMS]] 的标准式之间有十分简单的互译关系。 | |||
对于一个 <math>\mathrm{0-Y}</math> 标准表达式,作出其山脉图,但不考虑末列的影响,而是无限地逐行向上作出阶差序列,直到得到的序列全为 1。 | |||
现在你有了一个 <math>t\times{n}</math> 的山脉图,行标为 0 到 <math>t</math>,列标为 1 到 <math>n</math>。 | |||
定义 <math>b_{i,j}</math> 如下: | |||
* <math>x_{i,j}=1</math> 时 <math>b_{i,j}=0</math> | |||
*否则设 <math>x_{i,j}</math> 的父项为 <math>x_{i,k}</math>,令 <math>b_{i,j}=b_{i,k}+1</math> | |||
最后得到的矩阵 <math>(b_{i,j})</math> 删去最顶上全为 0 的行,并以水平线为轴镜像,即可得到等价的 <math>\mathrm{BMS}</math>。 | |||
对于一个 <math>\mathrm{BMS}</math> 标准式 <math>(d_{i,j})</math>(第 1 至第 <math>t</math> 行,第 1 至第 <math>n</math> 列),定义 <math>e_{i,j}</math> 如下: | |||
* <math>d_{i,j}=0</math> 时 <math>e_{i,j}=1</math> | |||
* 否则设 <math>d_{i,j}</math> 的父项为 <math>d_{i,k}</math>,令 <math>e_{i,j}=e_{i,k}+e_{i+1,j}</math>(如果 <math>i=t</math>,我们规定 <math>e_{i+1,j}=1</math>) | |||
最后取出 <math>f_k=e_{1,k}</math>,即为等价的 <math>\mathrm{0-Y}</math> 序列。 | |||
然而,尽管目前已有的分析均支持以上结论,目前对此尚未有严格的证明。 | |||
<math>\mathrm{BMS}</math> 和 <math>\mathrm{0-Y}</math> 的互相转换可以使用 [https://fiveyeargaokao.github.io/googology/bms-0y%E4%B8%80%E9%94%AE%E8%BD%AC%E6%8D%A2.html BMS 0-Y Converter Made By FiveYearGaoKao]。 | |||
== 与 [[Y序列|Y 序列]] 的关系 == | |||
<math>\mathrm{0-Y}</math> 虽然名字里带有 '''Y''',但它与 [[Y序列|Y 序列]]的内核有较大差异。 | |||
历史上,<math>\mathrm{0-Y}</math> 的出现晚于通常的 <math>\mathrm{Y}</math> 序列,而且强度也远低于 <math>\mathrm{Y}</math> 序列。事实上,<math>\mathrm{0-Y}</math> 是仿照 <math>\mathrm{BMS}</math> 制作出来的。 | |||
{{默认排序:序数记号}} | |||
[[分类:记号]] | [[分类:记号]] | ||
2025年8月30日 (六) 21:42的最新版本
定义
合法表达式
一个合法的 表达式是以 1 开头的正整数序列,即形如
的序列。
例如:和 都是合法的 表达式,而 不是。
结构
的合法表达式可分为零表达式、后继表达式和极限表达式。
- 零表达式指 的表达式,即空序列;
- 后继表达式指 的表达式,即末项为 1 的非空序列;
- 极限表达式指 的表达式,末项不为 1 的非空序列。
对于 的一个极限表达式 ,定义以下术语:
行标与列标
设想我们在一个无限大的矩阵下工作,从左往右是第 1,2,... 列,从下往上是第 0,1,... 行。第 行第 列的项记为 。
初始时,我们有 ,。
父项与阶差项
等于 1 的项没有父项。对于大于 1 的项,它的父项与它位于同一行,且是满足以下条件的最右侧项 :
- 且 。
- 如果 ,还要求 是 的祖先项。
这里“祖先项”的定义类似于 BMS:一个元素自己,以及它的父项、父项的父项、父项的父项的父项......共同构成它的祖先项。
对于 ,如果它有父项 ,则它的阶差项为 ;如果 ,则它的阶差项 。
由于第 行的项的阶差项构成了第 行,称第 行的序列是第 行的序列的阶差序列。
末列与坏根
第 列称为末列。
对于末列的某一项 ,它的父项设为 。如果在计算到某行(第 行)时有 ,则称 为坏根,称第 列为根列,并且不再计算第 行及之后的行。
以上给出了 极限表达式 的完整寻找坏根流程。
山脉图
要描述 的展开规则,需要用到山脉图的辅助。对于 的一个极限表达式 ,它的山脉图的画法如下:
先按照寻找坏根的规则画出第 0 到 行。现在你有了一个 的“矩阵”(第 0 至第 行,第 1 至第 列),接下来,对于第 行, 进行如下操作:
对于每个 ,用竖直线段连接 的下端与 的上端。这些竖直线段称为右腿, 称为它的端点。
对于每个大于 1 的 ,设 有父项 ,用斜线段连接 的下端与 的上端。这些斜线段称为左腿, 称为它的端点。
对第 1 到第 行各执行一次上述操作,就得到了 的山脉图。
山脉图有以下性质:从一个有父项的元素出发,沿右腿向上走一步,再沿左腿向下走一步,就能到达它的父项。
注意:有些情况下,山脉图只包含一行,即第 0 行。
注:由于山脉图的某一行只和其下的项有关,你也可以在逐行往上填写阶差序列的同时画出山脉图。许多常见的 教程都采用这个方法。
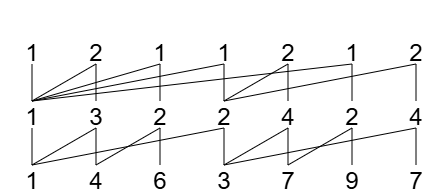
以 为例,其山脉图如右图所示。由于第2行末项2的阶差为1,故不再继续计算。
展开
对于 的一个表达式 :
- 如果它是零表达式,它对应序数 0。
- 如果它是后继表达式,它对应 的后继。
- 如果它是极限表达式,它的基本列第 项如下确定:
- 作出 的山脉图。称位于根列右侧的结构(包括阶差项和其对应的山脉图中的左右腿,不包括根列)为坏部,其余为好部。
- 删除坏部中第 行以下的所有项,并将 减 1。
- 接下来,保留山脉图的好部不动,将坏部平移并复制在山脉图末尾,复制 次。“坏部平移”是指左右腿及端点同时平移。
- 特别地,如果某一条左腿的端点位于根列左侧,复制时左腿的端点不向右平移。
- 接下来,你得到了根列右侧的一系列山脉图和第 行的一系列项。从根列右侧开始,从上到下,每一行从左到右,按照以下方式填入正整数:对于某个位置,向上通过右腿移动到值为 的项,然后向左下通过左腿移动到值为 的项,则回到初始位置并填上 。
- 最后得到的第 0 行的序列,就是 展开的基本列第 项。
的极限基本列是 ,从这个基本列中元素开始取前驱或取基本列所能得到的表达式是 0-Y 的标准式。
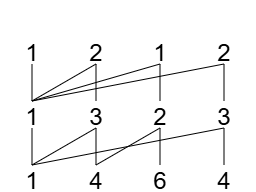
例 1:
先作出它的山脉图,从图中可以得到:根列为第 1 列,坏部为第 2、3、4 列。
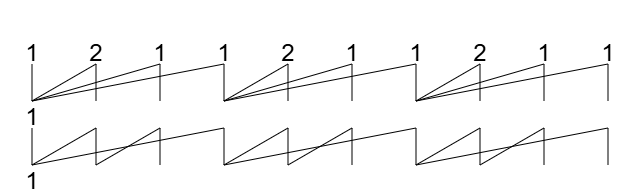
然后,将坏部第 2 行以下的数删除,并将其整体平移并复制 2 次。
接着,依次向山脉图中的“空位”填入正整数,注意所填的数满足“一个数等于其右腿和左腿连接的数之差”。
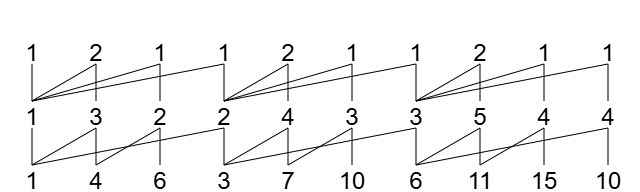
最后,根据山脉图的第 0 行,我们得到了 。
例 2:
其山脉图已经在前面给出。从图中可以得到:根列为第 4 列,坏部为第 5、6、7 列。
注意:第 2 行第 6 列的“1”的左腿的另一端(位于第 1 列)在根列左侧,故在复制时,其另一端点保持不动。
复制、填充后得到的山脉图如下。
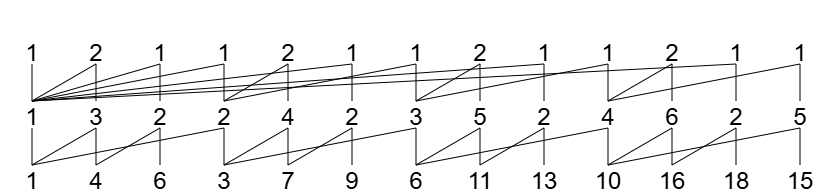
因此
枚举
我们使用 BMS 对 进行简单分析(左边是 ,右边是 )。
两者极限相等。
与 BMS 的互译
事实上, 与 BMS 的标准式之间有十分简单的互译关系。
对于一个 标准表达式,作出其山脉图,但不考虑末列的影响,而是无限地逐行向上作出阶差序列,直到得到的序列全为 1。
现在你有了一个 的山脉图,行标为 0 到 ,列标为 1 到 。
定义 如下:
- 时
- 否则设 的父项为 ,令
最后得到的矩阵 删去最顶上全为 0 的行,并以水平线为轴镜像,即可得到等价的 。
对于一个 标准式 (第 1 至第 行,第 1 至第 列),定义 如下:
- 时
- 否则设 的父项为 ,令 (如果 ,我们规定 )
最后取出 ,即为等价的 序列。
然而,尽管目前已有的分析均支持以上结论,目前对此尚未有严格的证明。
和 的互相转换可以使用 BMS 0-Y Converter Made By FiveYearGaoKao。
与 Y 序列 的关系
虽然名字里带有 Y,但它与 Y 序列的内核有较大差异。
历史上, 的出现晚于通常的 序列,而且强度也远低于 序列。事实上, 是仿照 制作出来的。